摘要訊息 : 進一步完善大數法則和由 Chebyshav 不等式得到的估計.

0. 前言

在《【機率論】初等機率論——Bernoulli 概型 : 大數法則》中, 我們介紹了 Chebyshav 不等式, 並且由它導出了大數法則和最小觀測次數. 然而, 我們在導出最小觀測次數的時候, 已經指出最小觀測次數 $\left \lceil \frac {1}{4\varepsilon\alpha} \right \rceil$ 是粗略的. 在本篇文章中, 我們將繼續討論, 得到盡可能精確的結論, 並且形成新的定理.

更新紀錄 :

• 2022 年 6 月 12 日進行第一次更新和修正.

1. De Moivre-Laplace 局部極限定理

考慮隨機變數 $\xi_{1}, \xi_{2}, ..., \xi_{n}$, 記 $S_{n} = \xi_{1} + \xi_{2} + ... + \xi_{n}$, 有 $\mathop {\mathrm {E}} \left ( \frac {S_{n}}{n} \right ) = p$. 由於 $\text {Var}(S_{n}) = npq$, 而 $\displaystyle {\begin {aligned} \text {Var}(S_{n}) &= \mathop {\mathrm {E}} \left ( (S_{n} - \mathop {\mathrm {E}}(S_{n}))^{2} \right ) = \mathop {\mathrm {E}} \left ( (S_{n} - np)^{2} \right ) \\ &= \mathop {\mathrm {E}} \left ( \left ( \frac {S_{n} - np}{n} \cdot n \right )^{2} \right ) = \mathop {\mathrm {E}} \left ( n^{2} \left ( \frac {S_{n} - np}{n} \right )^{2} \right ) \\ &= n^{2}\mathop {\mathrm {E}} \left ( \left ( \frac {S_{n}}{n} - p \right )^{2} \right ) = npq. \end {aligned}}$ 故有 $\mathop {\mathrm {E}} \left ( \left ( \frac {S_{n}}{n} - p \right )^{2} \right ) = \frac {pq}{n}$.

我們已經在大數法則中得到了 $\frac {Sn}{n}$ 與 $p$ 之間的機率意義. 那麼, 我們自然希望得到 $\left ( \frac {S_{n}}{n} - p \right )^{2}$ 與 $\frac {pq}{n}$ 的機率意義. 例如, 考慮下面這個機率 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq x\sqrt {\frac {pq}{n}} \right \}, x \in R}$ 如何?

又由於 $\mathop {\mathrm {E}}(S_{n}) = np$ 且 $\text {Var}(S_{n}) = npq$, 而 $\displaystyle {\frac {\left | \frac {S_{n}}{n} - p \right |}{\sqrt {\frac {pq}{n}}} = \frac {\left | \frac {S_{n}}{n} - p \right |}{\sqrt {\frac {pq}{n} \cdot \frac {n}{n}}} = \frac {\left | \sqrt {n^{2}}\frac {S_{n} - np}{n} \right |}{\sqrt {\frac {pq}{n}}} = \frac {\left | S_{n} - np \right |}{\sqrt {npq}} = \frac {\left | S_{n} - \mathop {\mathrm {E}}(S_{n}) \right |}{\sqrt {\text {Var}(S_{n})}}}.$ 我們又可以考慮 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n} - \mathop {\mathrm {E}}(S_{n})}{\sqrt {\text {Var}(S_{n})}} \right | \leq x \right \}},$ 如果對於 $n \geq 1$, 記 $P_{n}(k) = \binom {k}{n}p^{k}q^{n - k}$ ($k = 0, 1, 2, …, n$), 則有 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n} - \mathop {\mathrm {E}}(S_{n})}{\sqrt {\text {Var}(S_{n})}} \right | \leq x \right \} = \sum \limits_{\left \{ k : \frac {\left |k - np \right |}{\sqrt {npq}} \leq x \right \}}P_{n}(k)}.$ 那麼當 $n \to \infty$ 時, 機率 $P_{n}(k)$ 如何?

定理 1. (局部極限定理) 記 $P_{n}(k) = \binom {k}{n}p^{k}q^{n - k}\ (k = 0, 1, 2, ..., n)$, 設 $0 < p < 1$, 則對滿足 $\left | k - np \right | = o \left ( (npq)^{\frac {2}{3}} \right )$ 的所有 $k$, 一致有 $\displaystyle {P_{n}(k) \to \frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {(k - np)^{2}}{2npq}} \ (n \to \infty)}$ 即當 $n \to \infty$ 時, $\displaystyle {\sup \limits_{\left \{ k : \left | k - np \right | \leq \varphi(n) \right \}} \left \{ \left | \frac {P_{n}(k)}{\frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {(k - np)^{2}}{2npq}}} - 1 \right | \right \} \to 0}.$ 其中, $\varphi(n)$ 是任意滿足 $\varphi(n) = o \left ( (npq)^{\frac {2}{3}} \right )$ 的非負函數.

$證明$ :

根據 Stering 公式 (《複雜度下界》引理 1), 有 $\displaystyle {n! = \sqrt {2\pi n}\frac {n^{n}}{\mathrm {e}^{n}}(1 + R(n))}.$ 其中, 當 $n \to \infty$ 時, $R(n) \to 0$. 若 $n \to \infty$ 時, $k \to \infty, n - k \to \infty$, 則 $\displaystyle {\begin {aligned} \binom {k}{n} &= \frac {n!}{k!(n - k)!} \\ &= \frac {\sqrt {2\pi n}\left ( \frac {n}{e} \right )^{n}(1 + R(n))}{\sqrt {2\pi k \times 2\pi (n - k)}\left ( \frac {k}{e} \right )^{k}\left ( \frac {n - k}{e} \right )^{n - k}(1 + R(k))(1 + R(n - k))} \\ &= \frac {\frac {n^{n}}{\mathrm {e}^{n}}(1 + \varepsilon(n, k, n - k))}{\frac {1}{\sqrt {n}}\sqrt {2\pi k(n - k)}\frac {k^{k}}{\mathrm {e}^{k}}\frac {(n - k)^{n - k}}{\mathrm {e}^{n - k}}} \\ &= \frac {n^{n}(1 + \varepsilon(n, k, n - k))}{\sqrt {2\pi\frac {k}{n}(n - k)}k^{k}(n - k)^{n - k}} \\ &= \frac {n^{n}(1 + \varepsilon(n, k, n - k))}{\sqrt {2\pi\frac {k}{n}(n - k)}n^{k} \left ( \frac {k}{n} \right )^{k}n^{n - k} \left ( 1 - \frac {k}{n} \right )^{n - k}} \\ &= \frac {1}{\sqrt {2\pi n\frac {k}{n}\left ( 1 - \frac {k}{n} \right )}} \times \frac {1 + \varepsilon(n, k, n - k)}{\left ( \frac {k}{n} \right )^{k}\left ( 1 - \frac {k}{n} \right )^{n - k}}. \end {aligned}}$ 其中, 當 $n \to \infty, k \to \infty, n - k \to \infty$ 時, $\varepsilon(n, k, n - k) \to 0$. 故有 $\displaystyle {P_{n}(k) = \binom {k}{n}p^{k}q^{n - k} = \frac {p^{k}(1 - p)^{n - k} \left ( 1 + \varepsilon(n, k, n - k) \right )}{\sqrt {2\pi n\frac {k}{n} \left ( 1 - \frac {k}{n} \right ) \left ( \frac {k}{n} \right )^{k} \left ( 1 - \frac {k}{n} \right )^{n - k}}}}.$ 記 $\hat {p} = \frac {k}{n}$, 則 $\displaystyle {\begin {aligned} P_{n}(k) &= \binom {k}{n}p^{k}q^{n - k} = \frac {p^{k}(1 - p)^{n - k} \left ( 1 + \varepsilon(n, k, n - k) \right )}{\sqrt {2\pi n\hat {p} \left ( 1 - \hat {p} \right ) \hat {p}^{k} \left ( 1 - \hat {p} \right )^{n - k}}} \\ &= \frac {1 + \varepsilon(n, k, n - k)}{\sqrt {2\pi n\hat {p}\left ( 1 - \hat {p} \right )}}\left ( \frac {p}{\hat {p}} \right )^{k}\left ( \frac {1 - p}{1 - \hat {p}} \right )^{n - k} \\ &= \frac {1 + \varepsilon(n, k, n - k)}{\sqrt {2\pi n\hat {p}\left ( 1 - \hat {p} \right )}} \exp \left \{ k\ln {\frac {p}{\hat {p}} + (n - k)\ln {\frac {1 - p}{1 - \hat {p}}}} \right \} \\ &= \frac {1 + \varepsilon(n, k, n - k)}{\sqrt {2\pi n\hat {p}\left ( 1 - \hat {p} \right )}} \exp \left \{n \left (\frac {k}{n}\ln {\frac {p}{\hat {p}}} + \left ( 1- \frac {k}{n} \right )\ln {\frac {1 - p}{1 - \hat {p}}} \right )\right \} \\&= \frac {1 + \varepsilon(n, k, n - k)}{\sqrt {2\pi n\hat {p}\left ( 1 - \hat {p} \right )}}\exp \left \{-nH(\hat {p}) \right \} \\ &= \frac {1 + \varepsilon(n, k, n - k)}{\sqrt {2\pi n\hat {p}\left ( 1 - \hat {p} \right )}} \cdot \frac {1}{\mathrm {e}^{nH(\hat {p})}}. \end {aligned}}$ 其中, $H(x) = x\ln {\frac {x}{p}} + (1 - x)\ln {1 - x}{1 - p}$.

由於 $k$ 滿足 $\left | k - np \right | = o \left ( (npq)^{\frac {2}{3}} \right )$, 故當 $k \to \infty$ 時, $p - \hat {p} \to 0$. 另外, 對於 $0 < x < 1$, 有 $\displaystyle {H'(x) = \ln {\frac {x}{p}} - \ln {1 - x}{1 - p}, H''(x) = \frac {1}{x} + \frac {1}{1 - x}, H'''(x) = -\frac {1}{x^{2}} + \frac {1}{(1 - x)^{2}}}.$ 將 $H(\hat {p})$ 表示為 $H(p + (\hat {p} - p))$, 根據 Taylor 公式, 當 $n$ 充分大的時候, 有 $\displaystyle {\begin {aligned} H(\hat {p}) &= H(p) + H'(p)(\hat {p} - p) + \frac {1}{2}H''(p)(\hat {p} - p)^{2} + o(\left | \hat {p} - p \right |^{3}) \\ &= \frac {1}{2}\left ( \frac {1}{p} + \frac {1}{q} \right )\left ( \hat {p} - p \right )^{2} + o(\left | \hat {p} - p \right |^{3}). \end {aligned}}$ 從而有 $\displaystyle {P_{n}(k) = \frac {1 + \varepsilon(n, k, n - k)}{\sqrt {2\pi n\hat {p}(1 - \hat {p})}}\exp \left \{ -\frac {n}{2pq}\left ( \hat {p} - p \right )^{2} + n \cdot o \left ( \left | \hat {p} - p \right |^{3} \right ) \right \}}.$ 注意到 $\displaystyle {\frac {n}{2pq}\left ( \hat {p} - p \right )^{2} = \frac {n}{2pq}\left ( \frac {k}{n} - p \right )^{2} = \frac {(n - kp)^{2}}{2npq}},$ 故有 $\displaystyle {P_{n}(k) \to \frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {(k - np)^{2}}{2npq}}\left ( 1 + \varepsilon'(n, k, n - k) \right )}.$ 其中, $1 + \varepsilon'(n, k, n - k) = 1 + \varepsilon(n, k, n - k)\mathrm {e}^{n \cdot o(\left | \hat {p} - p \right |^{3})}\sqrt {\frac {p(1 - p)}{\hat {p}(1 - \hat {p})}}$. 顯然, 當 $n \to \infty$ 時, $\sup \left | \varepsilon'(n, k, n - k) \right | \to 0$. 因此, 有 $\displaystyle {P_{n}(k) \to \frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {(k - np)^{2}}{2npq}} \ (n \to \infty)}.$ 其中, $\left | k - np \right | \leq \varphi(n)$ 且 $\varphi(n) = o \left ( (npq)^{\frac {2}{3}} \right )$.

$\blacksquare$

推論 1. 對於一切 $x \in R$, 若 $x = o \left ( (npq)^{\frac {1}{6}} \right )$, 而 $np + x\sqrt {npq}$ 的結果是集合 $\left \{ 0, 1, 2, ..., n \right \}$ 中的整數, 則 $\displaystyle {P_{n}(np + x\sqrt {npq}) \to \frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {x^{2}}{2}} \ (n \to \infty)}.$ 即當 $n \to \infty$ 時, 有 $\displaystyle {\sup \limits_{\left \{ x : \left | x \right | \leq \psi(n) \right \}} \left \{ \left | \frac {P_{n}(np + x\sqrt {npq})}{\frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {x^{2}}{2}}} - 1 \right | \right \} \to 0}.$ 其中, $\psi(x) = o \left ((npq)^{\frac {1}{6}} \right )$.

在大數法則中, 我們曾給出 $\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \geq \varepsilon \right \} \to 0 \ (n \to \infty)$ 以質點游動的解釋. 引入上述理論之後, 我們可以將之前的解釋描述為 $\displaystyle {\mathop {\mathbf {P}} \left \{ S_{n} = k \right \} \to \frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {(k - np)^{2}}{2npq}}, \left | k - np \right | = o \left ( (npq)^{\frac {2}{3}} \right )}$ 和 $\displaystyle {\mathop {\mathbf {P}} \left \{ \frac {S_{n} - np}{\sqrt {npq}} = x \right \} \to \frac {1}{\sqrt {2\pi npq}\mathrm {e}^{-\frac {x^{2}}{2}}}, x = o \left ( (npq)^{\frac {1}{6}} \right )\ \ \ \ \ \ \ \ \ \ (\mathrm {I})}.$ 其中, $\mathop {\mathbf {P}} \left \{ \frac {S_{n} - np}{\sqrt {npq}} = x \right \}$ 中的 $np + x\sqrt {npq} \in \left \{ 0, 1, 2, ..., n \right \}$.

若設 $t_{k} = \frac {k - np}{\sqrt {npq}}$, $\Delta t_{k} = t_{k + 1} - t_{k} = \frac {1}{\sqrt {npq}},$, 那麼通過置換可以將 $(\mathrm {I})$ 式改寫為, $\displaystyle {\mathop {\mathbf {P}} \left \{ \frac {S_{n} - \mathop {\mathrm {E}}(S_{n})}{\sqrt {\text {Var}(S_{n})}} \right \} = t_{k} \to \frac {\Delta t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}}, t_{k} = o \left ( (npq)^{\frac {1}{6}} \right )}.$ 顯然, 當 $n \to \infty$ 時, $\displaystyle {\Delta t_{k} = \frac {1}{\sqrt {npq}} \to 0}.$ 根據上述描述, 我們發現 $\mathrm {e}^{-\frac {t_{k}^{2}}{2}} \cdot \Delta t_{k}$ 與定積分的定義類似, 於是我們自然想到 $\displaystyle {\mathop {\mathbf {P}} \left \{ a < \frac {S_{n} - \mathop {\mathrm {E}}(S_{n})}{\sqrt {\text {Var}(S_{n})}} \leq b \right \} = t_{k} \to \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x}, -\infty < a \leq b < +\infty}.$ 接下來, 我們將圍繞該式進行表述.

2. De Moivre-Laplace 極限定理

對於 $-\infty < a \leq b < +\infty$, 設 $\displaystyle {P_{n}(a, b] = \sum \limits_{a < x \leq b}P_{n}(np + x\sqrt {npq})},$ 其中求和是針對一切使得 $np + x\sqrt {npq}$ 為整數的 $x$ 求和. 由局部極限定理可見, 對於 $k = np + t_{k}\sqrt {npq}$ 決定且滿足 $\left | t_{k} \right | \leq T < +\infty$ 的 $t_{k}$, 由推論 1 有 $\displaystyle {P_{n}(np + t_{k}\sqrt {npq}) \to \frac {t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}}\big ( 1 + \varepsilon(t_{k}, n) \big )}.$ 其中, $\sup \limits_{\left | t_{k} \right | \leq T}\left | \varepsilon(t_{k}, n) \right | \to 0 \ (n \to \infty)$. 從而對於固定的 $a$ 和 $b$, 其中 $-\infty < -T \leq a \leq b \leq T < +\infty$, 有 $\displaystyle {\begin {aligned} \sum \limits_{a < t_{k} \leq b}P_{n}(np + t_{k}\sqrt {npq}) &= \sum \limits_{a < t_{k} \leq b}\frac {t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}} + \sum \limits_{a < t_{k} \leq b}\varepsilon(t_{k}, n)\frac {\Delta t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}} \\ &= \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + R_{n}^{(1)}(a, b) + R_{n}^{(2)}(a, b). \end {aligned}}$ 其中, $R_{1}^{(n)} = \sum \limits_{a < t_{k} \leq b}\frac {\Delta t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}} - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x}, R_{n}^{(2)} = \sum \limits_{a < t_{k} \leq b}\varepsilon(t_{k}, n)\frac {\Delta t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}}$. 對於 $R_{n}^{(1)}(a, b)$, 顯然地, 當 $n \to \infty$ 時, $\sup \limits_{-T \leq a \leq b \leq T}\left | R_{n}^{(1)}(a, b) \right | \to 0$. 為了繼續導出結論, 我們引入數學分析中的一個事實.

引理 1. $\frac {1}{\sqrt {2\pi}}\int_{-\infty}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} = 1$.

這個引理我們暫時不進行證明.

由於 $f(x) = \mathrm {e}^{-\frac {x^{2}}{2}}$ 是連續函數且 $f(x) > 0$, 故必有 $\displaystyle {\frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \leq \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \leq 1}.$ 因此, $\displaystyle {\begin {aligned} &\sup \limits_{-T \leq a \leq b \leq T}\left | R_{n}^{(2)}(a, b) \right | \\ &= \sup \limits_{-T \leq a \leq b \leq T}\left | \sum \limits_{a < t_{k} \leq b}\varepsilon(t_{k}, n)\frac {\Delta t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}} \right | \\ &= \sup \limits_{-T \leq a \leq b \leq T}\left | \sum \limits_{a < t_{k} \leq b}\varepsilon(t_{k}, n) \right |\frac {\Delta t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}} \\ &\leq \sup \limits_{\left | t_{k} \right | \leq T}\left | \varepsilon(t_{k}, n) \right | \sum \limits_{\left | t_{k} \right | \leq T}\frac {\Delta t_{k}}{\sqrt {2\pi}}\mathrm {e}^{-\frac {t_{k}^{2}}{2}} \\ &= \sup \limits_{-T \leq a \leq b \leq T}\left |\varepsilon(t_{k}, n) \right | \left ( R_{1}^{(n)}(a, b) + \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right ) \\ &= \sup \limits_{-T \leq a \leq b \leq T}\left |\varepsilon(t_{k}, n) \right | \sup \limits_{-T \leq a \leq b \leq T}R_{1}^{(n)}(a, b) + \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \\ &= \sup \limits_{-T \leq a \leq b \leq T} \left | \varepsilon(t_{k}, n) \right |. \end {aligned}}$ 所以, 當 $n \to \infty$ 時, $\sup \limits_{-T \leq a \leq b \leq T}\left |R_{n}^{(2)}(a, b) \right | \to 0$.

記 $\Phi(x) = \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{x}\mathrm {e}^{-\frac {t^{2}}{2}}dt$, 由上述過程可見 : $\displaystyle {\sup \limits_{-T \leq a \leq b \leq T}\left | P_{n}(a, b] - (\Phi(b) - \Phi(a)) \right | \to 0 \ (n \to \infty)}.$ 我們已經證明, 對於有限的 $T$, 上式成立. 那麼對於 $T \to \infty$, 上式是否也成立呢?

顯然, 對於任意給定的 $\varepsilon > 0$, 存在有限的 $T = T(\varepsilon)$ 使得 $\displaystyle {\frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} > 1 - \frac {\varepsilon}{4}}.$ 此時, 對於任意 $\varepsilon > 0$, 存在正整數 $N$, 使得對於一切 $n > N$ 和 $T = T(\varepsilon)$, 有 $\displaystyle {\sup \limits_{-T \leq a \leq b \leq T}\left | P_{n}(a, b] - (\Phi(b) - \Phi(a)) \right | < \frac {\varepsilon}{4}}.$ 結合 $P(a, b]$ 的定義與 $\frac {1}{2}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} > 1 - \frac {\varepsilon}{4}$, 必定有 $\displaystyle {P_{n}(-T, T] > 1 - \frac {\varepsilon}{2}}.$ 而 $P_{n}(-\infty, -T] + P_{n}(-T, T] + P_{n}(T, +\infty) = 1$. 因此, $\displaystyle {P_{n}(-\infty, -T] + P_{n}(T, +\infty) \leq \frac {\varepsilon}{2}}.$ 其中, $P_{n}(-\infty, T] = \lim \limits_{S \to -\infty}P_{n}(S, T], P_{n}(T, +\infty) = \lim \limits_{S \to +\infty}P_{n}(T, S]$. 這樣, 對於任意 $-\infty < a \leq -T \leq T \leq b < +\infty$, 根據絕對值不等式 (《【數學分析】實數——實數的四則運算》定理 3), 有 $\displaystyle {\begin {aligned} \left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | &= \Bigg | \left ( P_{n}(a, -T) - \frac {1}{\sqrt {2\pi}}\int_{a}^{-T} \mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right ) + \\ &\ \ \ \ \ \ \ \left ( P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T} \mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right ) + \\ &\ \ \ \ \ \ \ \left ( P_{n}(T, b] - \frac {1}{\sqrt {2\pi}}\int_{T}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right ) \Bigg | \\ &\leq \left | P_{n}(a, -T] - \frac {1}{\sqrt {2\pi}}\int_{a}^{-T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | + \\ &\ \ \ \ \ \left | P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | + \\ &\ \ \ \ \ \left | P_{n}(T, b] - \frac {1}{\sqrt {2\pi}}\int_{T}^{b}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right |. \end {aligned}}$ 顯然地, 我們有 $\displaystyle {P_{n}(a, -T] \leq P_{n}(-\infty, -T], P_{n}(T, b] \leq P_{n}(T, +\infty)}.$ 除此之外, 根據絕對值不等式, 我們又得 $\displaystyle {\left | P_{n}(a, -T] - \frac {1}{\sqrt {2\pi}}\int_{a}^{-T}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right |} \leq \left | P_{n}(a, -T] \right | + \left | \frac {1}{\sqrt {2\pi}\int_{a}^{-T}\mathrm {e}^{-\frac {x^{2}}{2}}}\mathrm {d}{x} \right |$ 和 $\displaystyle {\left | P_{n}(T, b] - \frac {1}{\sqrt {2\pi}}\int_{T}^{b}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right |} \leq \left | P_{n}(a, -T] \right | + \left | \frac {1}{\sqrt {2\pi}\int_{a}^{-T}\mathrm {e}^{-\frac {x^{2}}{2}}}\mathrm {d}{x} \right |.$ 因此, $\displaystyle {\begin {aligned} \left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | &\leq \left | P_{n}(-\infty, -T] \right | + \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{-T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + \\ &\ \ \ \ \ \left | P_{n}(T, +\infty) \right | + \frac {1}{\sqrt {2\pi}}\int_{T}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + \\ &\ \ \ \ \ \left | P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right |. \end {aligned}}$ 因為 $P_{n}(-\infty, -T] \geq 0, P_{n}(T, +\infty) \geq 0$, 於是 $\displaystyle {\begin {aligned} \left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | &\leq P_{n}(-\infty, -T] + \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{-T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + \\ &\ \ \ \ \ P_{n}(T, +\infty) + \frac {1}{\sqrt {2\pi}}\int_{T}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + \\ &\ \ \ \ \ \left | P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right |. \end {aligned}}$ 由於 $\frac {1}{\sqrt {2\pi}}\int_{-\infty}^{-T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + \frac {1}{\sqrt {2\pi}}\int_{T}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} = 1$ 且 $\frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} > 1 - \frac {\varepsilon}{4}$, 則 $\displaystyle {\frac {1}{\sqrt {2\pi}}\int_{-\infty}^{-T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} + \frac {1}{\sqrt {2\pi}}\int_{T}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \leq \frac {\varepsilon}{4}}.$ 結合 $P_{n}(-\infty, -T] + P(T, +\infty) \leq \frac {\varepsilon}{2}$, 那麼 $\displaystyle {\begin {aligned} \left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right | &\leq \frac {\varepsilon}{2} + \frac {\varepsilon}{4} + \left |P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right | \\ &= \frac {3}{4}\varepsilon + \left | P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right |. \end {aligned}}$ 對於 $\left | P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right |$, 我們已經知道 $P_{n}(-T, T] \geq 1 - \frac {\varepsilon}{2}, \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \geq 1 - \frac {\varepsilon}{4}$, 故 $\displaystyle {P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \geq -\frac {\varepsilon}{4}}.$ 不等式兩側取負, 不等式變號, 得到 $\displaystyle {- \left (P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right ) \leq \frac {\varepsilon}{4}}.$ 不等式兩側取絕對值, 有 $\displaystyle {\left | P_{n}(-T, T] - \frac {1}{\sqrt {2\pi}}\int_{-T}^{T}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right | \leq \frac {\varepsilon}{4}}.$ 綜上所述, $\displaystyle {\left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | \leq \frac {3}{4}\varepsilon + \frac {\varepsilon}{4} = \varepsilon}.$ 對於等號, 我們只需要適當放大 $\varepsilon$, 即可得到對於任意 $\varepsilon > 0$, 存在正整數 $N$, 當 $n > N$ 時, 有 $\displaystyle {\left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | < \varepsilon}.$ 根據極限的定義, 有 $\displaystyle {\lim \limits_{n \to \infty}P_{n}(a, b] = \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x}}.$ 我們總結一下上面的討論.

定理 2. (De Moivre - Laplace 積分定理) 設 $0 < p < 1$, $\displaystyle {P_{n}(k) = \binom {k}{n}p^{k}q^{n - k}, P_{n}(a, b] = \sum \limits_{a < x \leq b}P_{n}(np + x\sqrt {npq})}$ 那麼 $\displaystyle {\sup \limits_{-\infty < a \leq b < +\infty} \left \{ \left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right | \right \} \to 0 \ (n \to \infty)}.$

在大數法則中, 我們得到的 $\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \geq \varepsilon \right \} \to 0 \ (n \to \infty)$ 可以更精確地表示為 $\displaystyle {\sup \limits_{-\infty < a < b < +\infty} \left \{ \left | \mathop {\mathbf {P}} \left \{ a < \frac {S_{n} - \mathop {\mathrm {E}}(S_{n})}{\sqrt {\text {Var}(S_{n})}} \leq b \right \}- \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | \right \} \to 0 \ (n \to \infty)}.$ 由此可見, 對於任意 $-\infty < A < B < +\infty$, 有 $\displaystyle {\mathop {\mathbf {P}} \left \{ A < S_{n} \leq B \right \} - \left ( \Phi \left( \frac {B - np}{\sqrt {npq}} \right ) - \Phi \left( \frac {A - np}{\sqrt {npq}} \right ) \right ) \to 0 \ (n \to \infty)}.$

例題 1. 將規則的骰子擲 $12000$ 次. 問 : "6 點" 出現在次數區間 $(1800, 2100]$ 次的機率如何?

$解$ :

根據前面的討論, 我們可以寫出 $\displaystyle {\begin {aligned} P_{12000}(k) &= \sum \limits_{1800 < x \leq 2100}\binom {k}{12000} \left ( \frac {1}{6} \right )^{k}\left ( \frac {5}{6} \right )^{k} \\ &\doteq \Phi \left ( \frac {B - np}{\sqrt {npq}} \right ) - \Phi\left ( \frac {A - np}{\sqrt {npq}} \right ) \doteq 0.992. \end {aligned}}$ 其中, $A = 1800, B = 2100, n = 12000, p = \frac {1}{6}, q = \frac {5}{6}, \Phi(x) = \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{x}\mathrm {e}^{-\frac {t^{2}}{2}}\mathrm {d}{t}$.

$\blacksquare$

把二項機率 $P_{n}(np + x\sqrt {npq})$ (僅考慮能夠使得 $np + x\sqrt {npq}$ 取非負整數的 $x$) 標在圖上 :

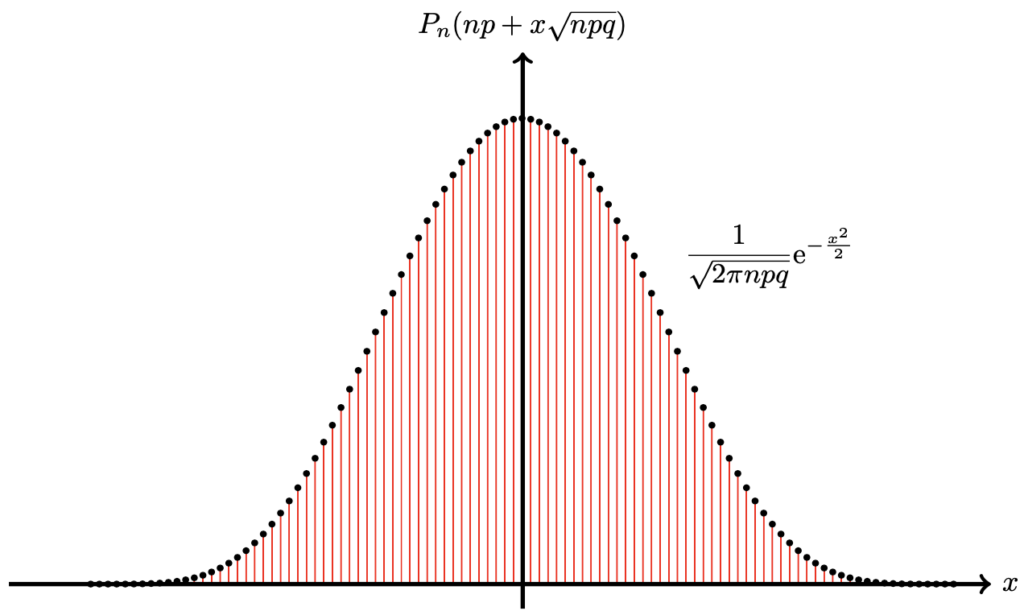
那麼局部定理表明, 對於 $x = o \left ( (npq)^{\frac {1}{6}} \right )$, 機率 $P_{n}(np + x\sqrt {npq})$ 的值比較好地位於函數 $f(x) = \frac {1}{\sqrt {2\pi npq}}\mathrm {e}^{-\frac {x^{2}}{2}}$ 的曲線上. 由積分定理可知, 機率 $P_{n}(a, b] = \mathop {\mathbf {P}} \left \{ a\sqrt {npq} < S_{n} - np \leq b \sqrt {npq} \right \} = \mathop {\mathbf {P}} \left \{ np + a\sqrt {npq} < S_{n} \leq np + b\sqrt {npq} \right \}$ 的值可以較好地由積分 $\frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x}$ 逼近.

記 $F_{n}(x) = P_{n}(-\infty, x] = \mathop {\mathbf {P}} \left \{ \frac {S_{n} - np}{\sqrt {npq}} \leq x \right \}$. 由 $\displaystyle {\sup \limits_{-\infty < a < b < +\infty}\left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \right | \to 0 \ (n \to \infty)}$ 可見 : $\displaystyle {\sup \limits_{-\infty < x < +\infty}\left | F_{n}(x) - \Phi(x) \right | \to 0 \ (n \to \infty)}.$ 那麼隨著 $n$ 的增長, $\sup \limits_{-\infty < a \leq b < +\infty}\left | P_{n}(a, b] - \frac {1}{\sqrt {2\pi}}\int_{a}^{b}\mathrm {e}^{\frac {x^{2}}{2}}\mathrm {d}{x} \right |$ 和 $\sup \limits_{-\infty < x < +\infty}\left | F_{n}(x) - \Phi(x) \right |$ 兩式趨向於 $0$ 的速度如何? 這裡直接引用 A.C. Berry - C.G. Esseen 定理的特殊情形 : $\displaystyle {\sup \limits_{-\infty < x < +\infty} \left | F_{n}(x) - \Phi(x) \right | \leq \frac {p^{2} + q^{2}}{\sqrt {npq}}}.$ 要特別強調的是, 估計 $\frac {1}{\sqrt {npq}}$ 的量級不能再提高了. 這裡指的是當 $p$ 的值接近於 $0$ 或者 $1$ 的時候, 甚至對於充分大的 $n$, 用函數 $\Phi(x)$ 來逼近 $F_{n}(x)$ 的效果也可能不太好. 因此, 產生了一個問題 : 當 $p$ 或者 $q$ 比較小的時候, 能否找到一個比局部定理和積分定理給出的更好的逼近呢? 為此, 我們指出, 當 $p = \frac {1}{2}$ 時, 二項分佈 $\left \{ P_{n}(k) \right \}$ 具有對稱的形狀. 不過當 $p$ 比較小的時候, 二項分佈的形狀不是對稱的, 不能指望用常態逼近有好的結果.

3. Poisson 定理

定理 3. (Poisson 定理) 設 $\displaystyle {P_{n}(k) = \begin {cases} \binom {k}{n}p^{k}q^{n - k} & {k = 0, 1, 2, …, n} \\ 0 & {k = n + 1, n + 2, …}. \end {cases}}$ 其中, $p$ 是關於 $n$ 的函數, 即 $p = p(n)$. 當 $n \to \infty$ 時, $p(n) \to 0$ 且 $np(n) \to \lambda$. 其中, $\lambda > 0$. 那麼, 對於任意 $k = 0, 1, 2, ...$, 有 $\displaystyle {P_{n}(k) \to \pi_{k} = \frac {\lambda^{k}\mathrm {e}^{-\lambda}}{k!}}.$

$證明$ :

根據條件, 我們構造 $\displaystyle {p(n) = \frac {\lambda}{n} + o \left ( \frac {1}{n} \right )}.$ 因此, 對於固定的 $k = 0, 1, 2, ...$ 和充分大的 $n$, $\displaystyle {\begin {aligned} P_{n}(k) &= \binom {k}{n}p^{k}q^{n - k} \\ &= \frac {n!}{k!(n - k)!}p^{k}q^{n - k} \\ &= \frac {n(n - 1)...(n - k - 1)}{k!}\left ( \frac {\lambda}{n} + o \left ( \frac {1}{n} \right ) \right )^{k}\left ( 1 - \left (\frac {\lambda}{n} + o \left ( \frac {1}{n} \right ) \right ) \right )^{n - k} \\ &= \frac {1}{k!} \cdot \frac {n(n - 1)...(n - k - 1)}{n^{k}}\left ( \lambda + o(1) \right )^{k}\left ( 1 - \left ( \frac {\lambda}{n} + o \left ( \frac {1}{n} \right ) \right ) \right )^{n - k}. \end {aligned}}$ 對於 $\frac {n(n - 1)...(n - k - 1)}{n^{k}}$, 有 $\displaystyle {\frac {\overbrace {(n - k - 1) \cdot (n - k - 1) \cdot ... \cdot (n - k - 1)}^{k \text { 個}}}{n^{k}} \leq \frac {n(n - 1)...(n - k - 1)}{n^{k}} \leq \frac {\overbrace {n \cdot n \cdot ... \cdot n}^{k \text { 個}}}{n^{k}}}.$ 由於 $\lim \limits_{n \to \infty}\frac {(n - k - 1)^{k}}{n^{k}} = \lim \limits_{n \to \infty}\frac {n^{k} + \sum \limits_{i = 1}^{k}\binom {i}{k}n^{i}(1 - k)^{k - i}}{n^{k}} = 1$ 且 $\lim \limits_{n \to \infty}\frac {n^{k}}{n^{k}} = 1$, 由夾擠定理可知 $\displaystyle {\lim \limits_{n \to \infty}\frac {n(n - 1)...(n - k - 1)}{n^{k}} = 1}.$ 那麼當 $n \to \infty$ 時, $\displaystyle {\frac {1}{k!} \cdot \frac {n(n - 1)...(n - k - 1)}{n^{k}}\left ( \lambda^{k} + o(1) \right )^{k} \to \lambda^{k}}.$ 而$\displaystyle {\begin {aligned} \lim \limits_{n \to \infty} \left ( 1 - \left (\frac {\lambda}{n} + o \left ( \frac {1}{n} \right ) \right ) \right )^{n - k} &= \lim \limits_{n \to \infty}\left (1 - \frac {\lambda}{n} + o \left ( \frac {1}{n} \right ) \right )^{n - k} \\ &= \lim \limits_{n \to \infty}\left ( 1 + \left (o\left ( \frac {1}{n} \right ) - \frac {\lambda}{n} \right ) \right )^{n - k} \\ &= \lim \limits_{n \to \infty}\left ( 1 + \left ( o \left ( \frac {1}{n} \right ) - \frac {\lambda}{n} \right ) \right )^{(n - k)\frac {o \left ( \frac {1}{n} \right ) - \frac {\lambda}{n}}{o \left ( \frac {1}{n} \right ) - \frac {\lambda}{n}}} \\ &= \mathrm {e}^{\lim \limits_{n \to \infty}(n - k)\left ( o \left ( \frac {1}{n} \right ) - \frac {\lambda}{n} \right )} \\ &= \mathrm {e}^{\lim \limits_{n \to \infty}(n - k) \cdot o \left ( \frac {1}{n} \right ) - (n - k)\frac {\lambda}{n}} \\ &= \mathrm {e}^{\lim \limits_{n \to \infty}-(n - k)\frac {\lambda}{n}} \\ &= \mathrm {e}^{\lim \limits_{n \to \infty}-\lambda + \frac {k}{n}\lambda} \\ &= \mathrm {e}^{-\lambda}. \end {aligned}}$ 故當 $n \to \infty$ 時, $P_{n}(k) \to \frac {\lambda^{k}\mathrm {e}^{-\lambda}}{k!}$.

綜上所述, 當 $n \to \infty$ 時, $p(n) \to 0$ 且 $np(n) \to \lambda$. 其中, $\lambda > 0$. 那麼, 對於任意 $k = 0, 1, 2, ...$, 有 $\displaystyle {P_{n}(k) \to \pi_{k} = \frac {\lambda^{k}\mathrm {e}^{-\lambda}}{k!}}.$

$\blacksquare$

序列 $\left \{ \pi_{k}, k = 0, 1, 2, ... \right \}$ 滿足 $\displaystyle {\pi_{k} > 0 \text { 且 } \sum \limits_{k = 0}^{\infty}\pi_{k} = 1},$ 因此可以作為機率分佈, 我們稱之為 Poisson 分佈 (Posson distribution). 之前所討論的所有分佈都是集中在有限個點上, Poisson 分佈時目前遇到的第一個集中在無限個點上的機率分佈.

和之前一樣, 我們仍然考慮當 $n \to \infty$ 時, 機率 $P_{n}(k)$ 收斂於 $\pi_{k}$ 的速度如何? 這裡直接給出一個不經證明的結論 : 若 $np(n) = \lambda$, 則 $\displaystyle {\sum \limits_{k = 0}^{\infty} \left | P_{n}(k) - \pi_{k} \right | \leq \frac {2\lambda}{n}\min \left \{ 2, \lambda \right \}}.$

4. De Moivre - Laplace 極限定理和大數法則

De Moivre - Laplace 極限定理和大數法則都是建立在 Bernoulli 概型上的, 那麼是否可以由 De Moivre - Laplace 極限定理導出大數法則呢?

因為 $\displaystyle {\begin {aligned} \mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} &= \mathop {\mathbf {P}} \left \{ \left | \frac {S_{n} - np}{n} \right | \leq \varepsilon \right \} \\ &= \mathop {\mathbf {P}} \left \{ \frac {\left | S_{n} - np \right |}{\sqrt {n} \cdot \sqrt {n}} \leq \varepsilon \right \} \\ &= \mathop {\mathbf {P}} \left \{ \frac {\left | S_{n} - np \right |}{\sqrt {n} \cdot \sqrt {n} \cdot \sqrt {pq}} \leq \frac {\varepsilon}{\sqrt {pq}} \right \} \\ &= \mathop {\mathbf {P}} \left \{ \frac {\left | S_{n} - np \right |}{\sqrt {npq}} \leq \sqrt {\frac {n}{pq}}\varepsilon \right \} \\ &= \mathop {\mathbf {P}} \left \{ \left | \frac {S_{n} - np}{\sqrt {npq}} \right | \leq \sqrt {\frac {n}{pq}}\varepsilon \right \} \\ &= \mathop {\mathbf {P}} \left \{-\varepsilon\sqrt {\frac {n}{pq}} \leq \frac {S_{n} - np}{\sqrt {npq}} \leq \varepsilon\sqrt {\frac {n}{pq}} \right \}, \end {aligned}}$ 根據 De Moivre - Laplace 極限定理, 當 $n \to \infty$ 時, 有 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \to \frac {1}{\sqrt {2\pi}}\int_{-\varepsilon\sqrt {\frac {n}{pq}}}^{\varepsilon\sqrt {\frac {n}{pq}}}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \to \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \to 1}.$ 即 $\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \to 1$. 這便是大數法則.

由上述的討論, 我們可以得到 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \to \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{+\infty}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} \ (n \to \infty)}.$ 然而, Chebyshev 不等式只能給出下面的估計 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \geq 1 - \frac {pq}{n\varepsilon^{2}}}.$ 在大數法則中, 為了得到使得 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \geq 1 - \alpha}$ 成立所需要的觀測次數, 我們由 Chebyshev 不等式得到了下面的估計 : $\displaystyle {n \geq \left \lfloor \frac {1}{4\varepsilon^{2}\alpha} \right \rfloor = n_{1}(\alpha)}.$ 現在, 我們可以通過 De Moivre - Laplace 極限定理得到更精確的估計. 我們由方程式 $\displaystyle {\frac {1}{\sqrt {2\pi}}\int_{-k(\alpha)}^{k(\alpha)}\mathrm {e}^{-\frac {x^{2}}{2}}\mathrm {d}{x} = 1 - \alpha}$ 求得 $k(\alpha)$. 由於 $\displaystyle {\varepsilon\sqrt {\frac {n}{pq}} \geq 2\varepsilon\sqrt {n}}$ 且根據不等式 $\displaystyle {2\varepsilon\sqrt {n} \geq k(\alpha)}$ 求出最小整數, 得到 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \geq 1 - \alpha}.$ 由 $2\varepsilon\sqrt {n} \geq k(\alpha)$ 可見 $\displaystyle {n = n_{2}(\alpha) = \left \lfloor \frac {k^{2}(\alpha)}{4\varepsilon^{2}} \right \rfloor}$ 可以保證 $\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \geq 1 - \alpha$ 成立, 其逼近精度可以由 $\displaystyle {\sup \limits_{-\infty < x < +\infty}\left | F_{n}(x) - \Phi(x) \right | \leq \frac {p^{2} + q^{2}}{\sqrt {npq}}}$ 得到.

例題 2. 設 $\varepsilon = 0.02$, $\alpha = 0.05$. 則基於 Chebyshev 不等式的估計觀測次數為 $12500$ 次, 而基於極限定理的估計觀測次數為 $2500$ 次.

5. 常態分佈

在 De Moivre - Laplace 積分定理中引入的函數 $\displaystyle {\Phi(x) = \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{x}\mathrm {e}^{-\frac {t^{2}}{2}}\mathrm {d}{t}}$ 在機率輪中有很大的作用, 稱為常態分佈函數 (normal distribution function) 或者 Gauss 分佈函數 (Gauss distribution function). 其導數 $\displaystyle {\varphi(x) = \frac {1}{\sqrt {2\pi}}\mathrm {e}^{-\frac {x^{2}}{2}}, x \in R}$ 稱為常態密度函數 (normal density function) 或者 Gauss 密度函數 (Gauss density function).

常態分佈屬於機率輪中另一種類型的分佈——連續分佈, 而我們之前討論的都是離散型分佈. 在相當一般的條件下, 大量獨立隨機變數 (未必是 Bernoulli 隨機變數) 之和的分佈可以很好地使用常態分佈來逼近.

函數 $\varphi(x) = \frac {1}{\sqrt {2\pi}}\mathrm {e}^{-\frac {x^{2}}{2}}$ 的圖形關於縱軸對稱, 且隨著 $\left | x \right | \to \infty$ 而趨於 $0$. 而函數 $\Phi(x) = \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{x}\mathrm {e}^{-\frac {t^{2}}{2}}\mathrm {d}{t}$ 隨著 $x \to +\infty$ 而趨於 $1$, 隨著 $x \to -\infty$ 而趨於 $0$.

除了 $\Phi(x)$ 之外, 我們還經常使用誤差函數 : $\displaystyle {\mathop {\mathrm {erf}}(x) = \frac {2}{\sqrt {\pi}}\int_{0}^{x}\mathrm {e}^{-t^{2}}\mathrm {d}{t}, x > 0}.$ 顯然, 對於 $x > 0$, 有 $\displaystyle {\Phi(x) = \frac {1}{2}\left ( 1 + \mathop {\mathrm {erf}} \left ( \frac {x}{\sqrt {2}} \right ) \right )}$ 和 $\displaystyle {\mathop {\mathrm {erf}}(x) = 2\Phi \left ( \sqrt {2}x \right ) - 1}.$

6. 成功頻率對機率的偏差滿足一定要求的試驗次數

在大數法則中, 我們曾指出, 由 Chebyshev 不等式給出的事件 $\left \{ \omega : \left | \frac {S_{n}}{n} - p \right | \geq \varepsilon \right \}$ 機率的估計是相當粗略的. 這一估計對於非負隨機變數 $X$, 是由 Chebyshev 不等式 $\displaystyle {\mathop {\mathbf {P}} \left \{ X \geq \varepsilon \right \} \leq \frac {\mathop {\mathrm {E}} \left (X^{2} \right )}{\varepsilon^{2}}}$ 得到的. 不過可以利用 Chebyshev 不等式的另一種形式 : $\displaystyle {\mathop {\mathbf {P}} \left \{ X \geq \varepsilon \right \} = \mathop {\mathbf {P}} \left \{ X^{2k} \geq \varepsilon^{2k} \right \} \leq \frac {\mathop {\mathrm {E}} \left ( X^{2k} \right )}{\varepsilon^{2k}}}.$ 然而, 還可以更進一步, 利用 Chebyshev 不等式的指數形式 : 對於 $X \geq 0$ 和 $\lambda > 0$, $\displaystyle {\mathop {\mathbf {P}} \left \{ X \geq \varepsilon \right \} = \mathop {\mathbf {P}} \left \{ \mathrm {e}^{\lambda x} \geq \varepsilon^{\lambda x} \right \} \leq \frac {\mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda x} \right )}{\mathrm {e}^{\lambda\varepsilon}} = \frac {\mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda x} \right )}{\mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda\varepsilon} \right )} = \mathop {\mathrm {E}} \left ( \frac {\mathrm {e}^{\lambda x}}{\mathrm {e}^{\lambda\varepsilon}} \right ) = \mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda(X - \varepsilon)} \right )}.$ 由於 $\lambda > 0$ 的任意性, 可見 $\displaystyle {\mathop {\mathbf {P}} \left \{ X \geq \varepsilon \right \} \leq \inf \limits_{\lambda > 0}\mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda(X - \varepsilon)} \right )}.$

接下來, 我們討論當 $X = \frac {S_{n}}{n}, S_{n} = \xi_{1} + \xi_{2} + ... + \xi_{n}, \mathop {\mathbf {P}} \left \{ \xi_{i} = 1 \right \} = p, \mathop {\mathbf {P}} \left \{ \xi_{i} = 0 \right \} = q, i = 1, 2, ..., n$ 時, 沿此路徑將會導致的結果.

記 $\varphi(\lambda) = \mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda \xi_{1}} \right )$, 則 $\displaystyle {\begin {aligned} \varphi(\lambda) &= \left . \mathrm {e}^{\lambda \xi_{1}} \right |_{\xi_{1} = 0}\mathop {\mathbf {P}} \left \{ \xi_{1} = 0 \right \} + \left . \mathrm {e}^{\lambda \xi_{1}} \right |_{\xi_{1} = 1}\mathop {\mathbf {P}} \left \{ \xi_{1} = 1 \right \} \\ &= 1 \times q + \mathrm {e}^{\lambda} \times p \\ &= 1 - p + p\mathrm {e}^{\lambda}. \end {aligned}}$ 對於兩兩獨立的隨機變數 $\xi_{1}, \xi_{2}, ..., \xi_{n}$, 則有 $\displaystyle {\begin {aligned} \mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda S_{n}} \right ) &= \mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda(\xi_{1} + \xi_{2} + ... + \xi_{n})} \right ) \\ &= \mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda\xi_{1} + \lambda\xi_{2} + ... + \lambda\xi_{n}} \right ) \\ &= \mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda\xi_{1}}\mathrm {e}^{\lambda\xi_{2}}...\mathrm {e}^{\lambda\xi_{n}} \right ) \\ &= \mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda\xi_{1}} \right )\mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda\xi_{2}} \right )...\mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda\xi_{n}} \right ) \\ &= \mathrm {e}^{n} \left ( \mathrm {e}^{\lambda\xi_{1}} \right ) \\ &= \varphi^{n}(\lambda). \end {aligned}}$ 因此, 對於 $0 < a < 1$, 根據 Chebyshev 不等式的指數形式, 有 $\displaystyle {\begin {aligned} \mathop {\mathbf {P}} \left \{ \frac {S_{n}}{n} \geq a \right \} &\leq \inf \limits_{\lambda > 0}\mathop {\mathrm {E}} \left ( \mathrm {e}^{\lambda \left ( \frac {S_{n}}{n} - a \right )} \right ) \\ &= \inf \limits_{\lambda > 0}\mathop {\mathrm {E}} \left ( \mathrm {e}^{\left ( \frac {\lambda}{n}S_{n} - \lambda a \right )} \right ) = \inf \limits_{\lambda > 0}\mathop {\mathrm {E}} \left ( \frac {\mathrm {e}^{\frac {\lambda}{n}S_{n}}}{\mathrm {e}^{\lambda a}} \right ) = \inf \limits_{\lambda > 0}\frac {\mathop {\mathrm {E}} \left ( \mathrm {e}^{\frac {\lambda}{n}S_{n}} \right )}{\mathrm {e}^{\lambda a}} \\ &= \inf \limits_{\lambda > 0}\frac {\varphi^{n} \left ( \frac {\lambda}{n} \right )}{\mathrm {e}^{\lambda a}} = \inf \limits_{\lambda > 0}\mathrm {e}^{-\lambda a} \cdot \varphi^{n} \left ( \frac {\lambda}{n} \right ) = \inf \limits_{\lambda > 0} \mathrm {e}^{-\lambda a}\mathrm {e}^{\ln {\varphi^{n} \left ( \frac {\lambda}{n} \right )}} \\ &= \inf \limits_{\lambda > 0}\mathrm {e}^{-\lambda a + n \ln {\varphi \left ( \frac {\lambda}{n} \right )}} = \inf \limits_{\lambda > 0}\mathrm {e}^{-n \left ( \frac {\lambda}{n}a - \ln {\varphi \left ( \frac {\lambda}{n} \right )} \right )} = \inf \limits_{\lambda > 0}\mathrm {e}^{-n \left (a\mu - \ln {\varphi(\mu)} \right )} \\ &= \mathrm {e}^{-n\sup \limits_{\mu > 0}a\mu - \ln {\varphi(\mu)}}. \end {aligned}}$ 其中, $\mu = \frac {\lambda}{n}$. 類似地, 也有 $\displaystyle {\mathop {\mathbf {P}} \left \{ \frac {S_{n}}{n} \leq a \right \} \leq \mathrm {e}^{-n\sup \limits_{\mu < 0}a\mu - \ln {\varphi(\mu)}}}.$ 當 $p \leq a \leq 1$ 時, 記函數 $f(x) = ax - \ln {\left ( 1 - p + p\mathrm {e}^{x} \right )}$, 則 $f'(x) = a - \frac {p\mathrm {e}^{x}}{1 - p + p\mathrm {e}^{2}}$. 令 $f'(x) = 0$, 得 $\displaystyle {\mathrm {e}^{x} = \frac {a(1 - p)}{p(1 - a)}}.$ 若 $x = x_{0}$ 使得 $f(x)$ 取得最大值, 則點 $x_{0}$ 滿足 $\mathrm {e}^{x_{0}} = \frac {a(1 - p)}{p(1 - a)}$. 因此, $\displaystyle {\sup \limits_{\mu > 0}f(\mu) = H(a)}.$ 其中, $H(a) = a\ln {\frac {a}{p}} + (1 - a)\ln {\frac {1 - a}{1 - p}}$. 這樣, 當 $p \leq a \leq 1$ 時, $\displaystyle {\mathop {\mathbf {P}} \left \{ \frac {S_{n}}{n} \geq a \right \} \leq \mathrm {e}^{-n\sup \limits_{\mu > 0}f(\mu)} = \mathrm {e}^{-nH(a)}.\ \ \ \ \ \ \ \ \ \ (\mathrm {II})}$ 而由於 $H(p + x) \geq 2x^{2}, 0 \leq p + x \leq 1$, 那麼對於任何 $\varepsilon > 0$ 和 $0 \leq p \leq 1$, 有 $\displaystyle {\mathop {\mathbf {P}} \left \{ \frac {S_{n}}{n} - p \geq \varepsilon \right \} \leq \mathrm {e}^{-2n\varepsilon^{2}}.\ \ \ \ \ \ \ \ \ \ (\mathrm {III})}$ 類似可得, 當 $a \leq p \leq 1$ 時, $\displaystyle {\mathop {\mathbf {P}} \left \{ \frac {S_{n}}{n} \leq a \right \} \leq \mathrm {e}^{-nH(a)}}.\ \ \ \ \ \ \ \ \ \ (\mathrm {IV})$ 從而對於任意 $\varepsilon > 0$ 和 $0 \leq p \leq 1$, 有 $\displaystyle {\mathop {\mathbf {P}} \left \{ \frac {S_{n}}{n} - p \leq -\varepsilon \right \} \leq \mathrm {e}^{-2n\varepsilon^{2}}.\ \ \ \ \ \ \ \ \ \ (\mathrm {V})}$ 於是, $\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \leq 2\mathrm {e}^{-2n\varepsilon^{2}}$. 由此可見, 對於任意 $0 \leq p \leq 1$, 保證不等式 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \geq 1 - \alpha}$ 成立的估計觀測次數 $n_{3}(\alpha)$ 決定於 $\displaystyle {n_{3}(\alpha) = \left \lfloor \frac {\ln {\frac {2}{\alpha}}}{2\varepsilon^{2}} \right \rfloor}.$ 若不取整數部分, 直接將 $n_{3}(\alpha)$ 於 $n_{1}(\alpha) = \left \lfloor \frac {1}{4\alpha\varepsilon^{2}} \right \rfloor$ 比較可見 : $\displaystyle {\frac {n_{1}(\alpha)}{n_{3}(\alpha)} = \frac {\frac {1}{4\alpha\varepsilon^{2}}}{\frac {\ln {\frac {2}{\alpha}}}{2\varepsilon^{2}}}} = \frac {1}{2\alpha\ln {\frac {2}{\alpha}}} \to +\infty \ (\alpha \to 0^{+}).$ 由此可見, 當 $\alpha \to 0^{+}$ 時, 由 Chebyshev 不等式的指數形式估計最小必須要觀測的次數, 比用一般的 Chebyshev 不等式估計的次數更加精確, 特別是對於比較小的 $\alpha$.

利用數學分析中的結論 $\displaystyle {\lim \limits_{x \to -\infty}\frac {1}{\sqrt {2\pi}}\int_{x}^{+\infty}\mathrm {e}^{-\frac {t^{2}}{2}}\mathrm {d}{t} = \frac {1}{\sqrt {2\pi}x}\mathrm {e}^{-\frac {x^{2}}{2}}},$ 可以證明當 $\alpha \to o^{+}$ 時, $k^{2}(\alpha) \to 2 \ln {\frac {2}{\alpha}}$. 於是有 $\displaystyle {\lim \limits_{\alpha \to 0^{+}}\frac {n_{2}(\alpha)}{n_{3}(\alpha)} = 1}.$ 式 $(\mathrm {II}), (\mathrm {III}), (\mathrm {IV}), (\mathrm {V})$ 和式 $\displaystyle {\mathop {\mathbf {P}} \left \{ \left | \frac {S_{n}}{n} - p \right | \leq \varepsilon \right \} \leq 2\mathrm {e}^{-2n\varepsilon^{2}}}\ \ \ \ \ \ \ \ \ \ (\mathrm {VI})$ 合稱為大偏差機率的不等式 (inequalities for the probability of large deviations). 利用 De Moivre - Laplace 定理, 可以簡單地對事件 $\left \{ \left | S_{n} - np \right | \leq x\sqrt {n} \right \}$ 的機率進行估計. 此事件表示 $S_{n}$ 對 $np$ (數量級為 $\sqrt {n}$) 的標準離差 (standard deviation). 而不等式 $(\mathrm {III}), (\mathrm {V})$ 和 $(\mathrm {VI})$ 對 $\displaystyle {\left \{ \left | S_{n} - np \right | \leq x\sqrt {n} \right \}}$ 給出的估計描繪量級大於 $\sqrt {n}$ 的離差, 其數量級為 $n$.

7. 練習題

自主習題 1. 設 $p = \frac {1}{2}$, 而 $Z_{n} = 2S_{n} - n$ ($n$ 組試驗中的 $1$ 比 $0$ 多出的數量). 證明 : $\displaystyle {\sup \limits_{j}\left | \sqrt {\pi n}\mathop {\mathbf {P}} \left \{ Z_{2n} = j - \mathrm {e}^{-\frac {j^{2}}{4^{n}}} \right \} \right | \to 0 \ (n \to \infty)}.$

自主習題 2. 證明 : Poisson 定理對於 $p = \frac {\lambda}{n}$ 的收斂速度為 $\displaystyle {\sup \limits_{k}\left | P_{n}(k) - \frac {\lambda^{k}\mathrm {e}^{-\lambda}}{k!} \right | \leq \frac {\lambda^{2}}{n}}.$