摘要訊息 : 從結果來估計成功的機率.

0. 前言

在這篇文章中, 我們將基於大數法則 (《【機率論】初等機率論——Bernoulli 概型 : 大數法則》) 引入統計學中的幾個概念. 部分概念其實我們在《機器學習筆記》中已經解釋過了, 只不過這次我們從機率輪和統計學的角度更加嚴格地重新審視這些概念.

更新紀錄 :

• 2022 年 6 月 16 日進行第一次更新和修正.

1. "成功" 機率估計的概念及其性質

我們之前所討論的 Bernoulli 概型 (\Omega, \mathscr {A}, \mathbf {P}) : \displaystyle {\begin {aligned} &\Omega = \left \{ \omega : \omega = (x_{1}, x_{2}, ..., x_{n}), x_{i} \in \left \{ 0, 1 \right \}, i = 1, 2, ..., n \right \}, \\ &\mathscr {A} = \left \{ A : A \subseteq \Omega \right \}, \mathop {\mathbf {P}} \left ( \left \{ \omega \right \} \right ) = p(\omega) = p^{\sum \limits_{i}x_{i}}(1 - p)^{n - \sum \limits_{i}x_{i}} \end {aligned}} 都是假設 p 的值已知, 也就是我們已經知道試驗 "成功" 的機率. 現在假設 p 事先未知, 但是我們知道試驗結局的觀測結果, 或是對隨機變數 \xi_{1}(\omega), \xi_{2}(\omega), ..., \xi_{n}(\omega) 的觀測結果來確定機率 p. 其中, \xi_{i}(\omega) = x_{i} (i = 1, 2, ..., n). 這便是統計學中的經典問題之一, 它有多種不同的提法.

在《機器學習筆記》中, 若只有一個參數, 那麼我們通常使用 \theta, 這也是統計學中對未知參數慣用的記號. 我們沿用這個記號, 也就是把 p 記為 \theta, 並且認為 \theta 是事前的 (priori). 對於機率 p 來說, 必定有 p \in [0, 1], 對於 \theta 來說也是類似. 我們認為要估計的 \theta 有 \displaystyle {\theta \in \Theta = [0, 1]}. 通常來說, 我們可以將這樣的統計學模型寫為 \displaystyle {\mathscr {E} = (\Omega, \mathscr {A}, \mathop {\textbf {P}}, \theta \in \Theta), \mathop {\textbf {P}}_{\theta} \left ( \left \{ \omega \right \} \right ) = \theta^{\sum \limits_{i}x_{i}}}(1 - \theta)^{n - \sum \limits_{i}x_{i}}. 而任意在 \Theta 中取值的函數, 即值域 R_{T} 滿足 R_{T} \subseteq \Theta 的函數 T_{n} = T_{n}(\omega) 稱為估計量 (estimator).

定義 1. 若對於任意 \varepsilon > 0 和 \theta \in \Theta, 估計量 T_{n}^{*} 滿足 \displaystyle {\mathop {\textbf {P}}_{\theta} \left \{ \left | T_{n}^{*} - \theta \right | \geq \varepsilon \right \} \to 0\ (n \to \infty)}, 我們稱估計量 T_{n}^{*} 是相合的 (consistent).

如果設 S_{n} = \xi_{1} + \xi_{2} + ... + \xi_{n}, T_{n}^{*} = \frac {S_{n}}{n}, 則由大數法則可知 \displaystyle {\mathop {\textbf {P}}_{\theta} \left \{ \left | \frac {S_{n}}{n} - \theta \right | \geq \varepsilon \right \} \to 0\ (n \to \infty)}. 顯然, T_{n}^{*} 是相合的.

定義 2. 若對於任意 \theta \in \Theta, 估計量 T_{n}^{*} 滿足 \displaystyle {\mathop {\mathrm {E}}_{\theta}(T_{n}^{*}) = \theta}, 那麼我們稱估計量 T_{n}^{*} 是無偏的 (unbiased).

估計量的無偏性是一條很自然的性質. 因為任何合理的估計量, 至少在平均意義下都應當得到期望的結果. 不過, 無偏的估計量並不是唯一的. 例如, 對於任意滿足 b_{1} + b_{2} + ... + b_{n} = n 的估計量 \displaystyle {T_{n} = \frac {b_{1}\xi_{1} + b_{2}\xi_{2} + ... + b_{n}\xi_{n}}{n}} 都是無偏的. 我們可以容易地從 \displaystyle {\begin {aligned} \mathop {\mathrm {E}}_{\theta}(T_{n}) &= \mathop {\mathrm {E}}_{\theta} \left ( \frac {b_{1}\xi_{1} + b_{2}\xi_{2} + ... + b_{n}\xi_{n}}{n} \right ) \\ &= \frac {1}{n} \mathop {\mathrm {E}}_{\theta}(b_{1}\xi_{1} + b_{2}\xi_{2} + ... + b_{n}\xi_{n}) \\ &= \frac {1}{n} \big ( \mathop {\mathrm {E}}_{\theta}(b_{1}\xi_{1}) +\mathop {\mathrm {E}}_{\theta}(b_{2}\xi_{2}) + ... + \mathop {\mathrm {E}}_{\theta}(b_{n}\xi_{n}) \big ) \\ &= \frac {1}{n}\big ( b_{1}\mathop {\mathrm {E}}_{\theta}(\xi_{1}) + b_{2}\mathop {\mathrm {E}}_{\theta}(\xi_{2}) + ... + b_{n}\mathop {\mathrm {E}}_{\theta}(\xi_{n}) \big ) \\ &= \frac {1}{n} \left ( b_{1}\theta + b_{2}\theta + ... + b_{n}\theta \right ) \\ &= \frac {\theta}{n}(b_{1} + b_{2} + ... + b_{n}) = \theta \end {aligned}} 看出. 至少對於有限的 b_{i}\ (i = 1, 2, ..., n), 即 \left | b_{i} \right | \leq K < +\infty, 這些估計量都服從大數法則. 從而對於 T_{n}^{*} = \frac {S_{n}}{n} (因為 \mathop {\mathrm {E}}(S_{n}) = np) 和 T_{n} 這兩個估計量, 它們都是無偏的估計量.

這樣, 就產生了一個問題 : 對於不同的無偏估計量, 哪一個是最好的, 最佳的? 不過, 根據估計量本身的含義, 自然是 T_{n} 和 \theta 相差越小越好. 於是, 自然地, 我們想到了使用方差來度量.

定義 3. 考慮所有可能的無偏估計 T_{n} 的集合 \left \{ T_{n} \right \}, 我們認為 \widetilde {T_{n}} \in \left \{ T_{n} \right \} 是有效的 (efficient), 若且唯若 \displaystyle {\mathop {\mathrm {Var}}_{\theta}(\widetilde {T_{n}}) = \inf \limits_{T_{n}} \left \{ \mathop {\mathrm {Var}}_{\theta}(T_{n}) \right \}} 成立. 其中, \theta \in \Theta.

斷言 1. 設 S_{n} = \xi_{1} + \xi_{2} + ... + \xi_{n}, T_{n}^{*} = \frac {S_{n}}{n}, 則 T_{n}^{*} 是關於未知參數 \theta 的有效估計量.

證明 :

事實上, 我們有 \displaystyle {\mathop {\mathrm {Var}}_{\theta}(T_{n}^{*}) = \mathop {\mathrm {Var}}_{\theta} \left ( \frac {S_{n}}{n} \right ) = \frac {\mathop {\mathrm {Var}}_{\theta}(S_{n})}{n^{2}} = \frac {n\theta(1 - \theta)}{n^{2}} = \frac {\theta(1 - \theta)}{n}}. 因此, 為了證明估計量 T_{n}^{*} 是有效的, 只需要證明 \displaystyle {\inf \limits_{T_{n}} \left \{ \mathop {\mathrm {Var}}_{\theta}(T_{n}) \right \} \geq \frac {\theta(1 - \theta)}{n}}.

對於 \theta = 0 和 \theta = 1, 不等式顯然成立, 因為方差永遠不會小於零. 現在設 \theta \in (0, 1) 且 p_{\theta}(x_{i}) = \theta^{x_{i}}(1 - \theta)^{1 - x_{i}}. 顯然, \displaystyle {\mathop {\textbf {P}}_{\theta} \left ( \left \{ \omega \right \} \right ) = p_{\theta}(\omega) = \prod \limits_{i = 1}^{n}p_{\theta}(x_{i})}.

記 L_{\theta}(\omega) = \ln {p_{\theta}(\omega)}, 那麼有 \displaystyle {\begin {aligned} L_{\theta}(\omega) &= \ln {p_{\theta}(\omega)} = \ln {p_{\theta}(x_{1}) \cdot p_{\theta}(x_{2}) \cdot ... \cdot p_{\theta}(x_{n})} \\ &= \ln {p_{\theta}(x_{1})} + \ln {p_{\theta}(x_{2})} + ... + \ln {p_{\theta}(x_{n})} \\ &= \ln {\theta^{x_{1}}(1 - \theta)^{1 - x_{1}}} + \ln {\theta^{x_{2}}(1 - \theta)^{1 - x_{2}}} + ... + \ln {\theta^{x_{n}}(1 - \theta)^{1 - x_{n}}} \\ &= \ln {\theta^{x_{1}}} + \ln {(1 - \theta)^{1 - x_{1}}} + \ln {\theta^{x_{2}}} + \ln {(1 - \theta)^{1 - x_{2}}} + ... + \ln {\theta^{x_{n}}} + \ln {(1 - \theta)^{1 - x_{n}}} \\ &= x_{1}\ln {\theta} + (1 - x_{1})\ln {(1 - \theta)} + x_{2}\ln {\theta} + (1 - x_{2})\ln {(1 - \theta)} + ... + \\ &\quad x_{n}\ln {\theta} + (1 - x_{n})\ln {(1 - \theta)} \\ &= (x_{1} + x_{2} + ... + x_{n})\ln {\theta} + \big ( (1 - x_{1}) + (1 - x_{2}) + ... + (1 - x_{n}) \big )\ln {(1 - \theta)} \\ &= \sum \limits_{i = 1}^{n}x_{i}\ln {\theta} + \sum \limits_{i = 1}^{n}(1 - x_{i})\ln {(1 - \theta)}. \end {aligned}} 對 \theta 求導數可得 \displaystyle {\begin {aligned} \frac {\partial L_{\theta}(\omega)}{\partial \theta} &= \frac {\sum \limits_{i = 1}^{n}x_{i}}{\theta} - \frac {\sum \limits_{i = 1}^{n}(1 - x_{i})}{1 - \theta} \\ &= \frac {\sum \limits_{i = 1}^{n}(1 - \theta) - \theta\sum \limits_{i = 1}^{n}(1 - x_{i})}{\theta(1 - \theta)} \\ &= \frac {\sum \limits_{i = 1}^{n}x_{i} - \theta\sum \limits_{i = 1}^{n}x_{i} - \theta\sum \limits_{i = 1}^{n}1 + \theta\sum \limits_{i = 1}^{n}x_{i}}{\theta(1 - \theta)} \\ &= \frac {\sum \limits_{i = 1}^{n}x_{i} - \sum \limits_{i = 1}^{n}\theta}{\theta(1 - \theta)} \\ &= \frac {x_{1} + x_{2} + ... + x_{n} - \overbrace {\theta - \theta - ... - \theta}^{n\ \text {個}\ \theta}}{\theta(1 - \theta)} \\ &= \frac {(x_{1} - \theta) + (x_{2} - \theta) + ... +(x_{n} - \theta)}{\theta(1 - \theta)} \\ &= \frac {\sum \limits_{i = 1}^{n}(x_{i} - \theta)}{\theta(1 - \theta)}. \end {aligned}}

我們注意到 1 \equiv \sum \limits_{\omega}p_{\theta}(\omega). 等式兩側對 \theta 求導數可得 \displaystyle {0 = \sum \limits_{\omega}\frac {\partial p_{\theta}(\omega)}{\partial \theta}\ \ \ \ \ \ \ \ \ \ (\mathrm {I})}. 另外, L_{\theta}(\omega) = \ln {p_{\theta}(\omega)} 對 \theta 的偏導數可以表示為 \displaystyle {\frac {\partial L_{\theta}(\omega)}{\partial \theta} = \frac {1}{p_{\theta}(\omega)} \cdot \frac {\partial p_{\theta}(\omega)}{\partial \theta}}. 對式 (\mathrm {I}) 進行變幻並且根據期望的定義可得 \displaystyle {0 = \sum \limits_{\omega}\frac {\partial p_{\theta}(\omega)}{\partial \theta} = \sum \limits_{\omega}\frac {\frac {\partial p_{\theta}(\omega)}{\partial \theta(\omega)}}{p_{\theta}(\omega)}p_{\theta}(\omega) = \mathop {\mathrm {E}}_{\theta} \left ( \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ). \ \ \ \ \ \ \ \ \ \ (\mathrm {II})}

我們還注意到一個可以利用的信息, 即 T_{n} 都是無偏的, 亦即有 \displaystyle {\theta = \mathop {\mathrm {E}}_{\theta}(T_{n})}. 根據期望的定義, 上式還可以進一步展開 : \displaystyle {\theta = \mathop {\mathrm {E}}_{\theta}(T_{n})} = \sum \limits_{\omega}T_{n}(\omega)p_{\theta}(\omega). 等式兩側對 \theta 求導數可得 \displaystyle {1 = \sum \limits_{\omega}T_{n}(\omega)\frac {\partial p_{\theta}(\omega)}{\partial \theta} = \sum \limits_{\omega}T_{n}(\omega)\frac {\frac {\partial p_{\theta}(\omega)}{\partial \theta}}{p_{\theta}(\omega)}p_{\theta}(\omega) = \mathop {\mathrm {E}}_{\theta}\left ( T_{n}(\omega)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ). \ \ \ \ \ \ \ \ \ \ (\mathrm {III})}

我們再次對式 (\mathrm {II}) 進行變換, 等式兩側乘以 \theta, 得 \displaystyle {0 \equiv 0 \cdot \theta = \theta \cdot \mathop {\mathrm {E}}_{\theta} \left ( \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) = \mathop {\mathrm {E}}_{\theta} \left ( \theta \cdot \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right )}. 然後結合上式和式 (\mathrm {III}), 就有 \displaystyle {\begin {aligned} 1 &\equiv 1 - 0 = \mathop {\mathrm {E}}_{\theta} \left ( T_{n}\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) - \mathop {\mathrm {E}}_{\theta} \left ( \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) \\ &= \mathop {\mathrm {E}}_{\theta} \left ( T_{n}\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) - \mathop {\mathrm {E}}_{\theta} \left ( \theta\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) \\ &= \mathop {\mathrm {E}}_{\theta} \left ( T_{n}\frac {\partial L_{\theta}(\omega)}{\partial \theta} - \theta\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) \\ &= \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ). \end {aligned}} 那麼, \displaystyle {1 = \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) = \left | \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) \right | = \left | 1 \right |}. 結合《【機率論】初等機率論——隨機變數及其特徵》中期望的性質和 Cauchy-Schwarz 不等式的機率形式, 我們可以得到 \displaystyle {\begin {aligned} 1 = \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) &= \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right )\mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) \\ &= \left | \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) \right | \cdot \left | \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right ) \right | \\ &\leq \mathop {\mathrm {E}}_{\theta} \left ( \left | (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right | \right ) \mathop {\mathrm {E}}_{\theta} \left ( \left | (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right | \right ) \\ &= \left ( \mathop {\mathrm {E}}_{\theta} \left ( \left | (T_{n} - \theta)\frac {\partial L_{\theta}(\omega)}{\partial \theta} \right | \right ) \right )^{2} \\ &\leq \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)^{2} \right ) \mathop {\mathrm {E}}_{\theta} \left ( \left ( \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right )^{2} \right ). \end {aligned}} 記 I_{n}(\theta) = \mathop {\mathrm {E}}_{\theta} \left ( \left ( \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right )^{2} \right ), 有 \displaystyle {1 \leq \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)^{2} \right ) \cdot I_{n}(\theta)} \Leftrightarrow \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)^{2} \right ) \geq \frac {1}{I_{n}(\theta)}.

總之, 我們可以得到 \displaystyle {\mathop {\mathrm {Var}}_{\theta}(T_{n}) = \mathop {\mathrm {E}}_{\theta} \left ( (T_{n} - \theta)^{2} \right ) \geq \frac {1}{I_{n}(\theta)}}. 這是 C. R. Rao - G. Cramér 不等式的特殊形式, 對於我們所要討論的形式, 有 \displaystyle {\begin {aligned} I_{n}(\theta) &= \mathop {\mathrm {E}}_{\theta} \left ( \left ( \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right )^{2} \right ) \\ &= \mathop {\mathrm {E}}_{\theta} \left ( \left ( \frac {\sum \limits_{i = 1}^{n} \big ( \xi_{i}(\omega) - \theta \big )}{\theta(1 - \theta)} \right )^{2} \right ) \\ &= \mathop {\mathrm {E}}_{\theta} \left ( \frac {\left (\xi_{1}(\omega) + \xi_{2}(\omega) + ... + \xi_{n}(\omega) - \overbrace {n - n - ... - n}^{n\ \text {個}\ \theta} \right )^{2}}{\big ( \theta(1 - \theta) \big )^{2}} \right ) \\ &= \mathop {\mathrm {E}}_{\theta} \left ( \frac {\left (\xi_{1}(\omega) + \xi_{2}(\omega) + ... + \xi_{n}(\omega) - n\theta \right )^{2}}{\big ( \theta(1 - \theta) \big )^{2}} \right ) \\ &= \frac {1}{\big ( \theta(1 - \theta) \big )^{2}} \mathop {\mathrm {E}}_{\theta} \left ( \left (\xi_{1}(\omega) + \xi_{2}(\omega) + ... + \xi_{n}(\omega) + n\theta \right )^{2} \right ) \\ &= \frac {n \big ( \theta(1 - \theta) \big )}{\big ( \theta(1 - \theta) \big )^{2}} = \frac {n}{\theta(1 - \theta)}. \end {aligned}} 最終, 我們有 \displaystyle {\inf \limits_{T_{n}} \left \{ \mathop {\mathrm {Var}}_{\theta}(T_{n}) \right \} \geq \frac {\theta(1 - \theta)}{n}}.

綜上所述, T_{n}^{*} 是關於未知參數 \theta 的有效估計量.

\blacksquare

在斷言 1 的證明中, 我們所記的 \displaystyle {I_{n}(\theta) = \mathop {\mathrm {E}}_{\theta} \left (\left ( \frac {\partial L_{\theta}(\omega)}{\partial \theta} \right )^{2} \right )} 被稱為 Fisher 信息量 (Fisher's information).

Tip : 至於斷言 1 證明中的最後部分 \displaystyle {\mathop {\mathrm {E}}_{\theta} \left ( \left (\xi_{1}(\omega) + \xi_{2}(\omega) + ... + \xi_{n}(\omega) + n\theta \right )^{2} \right ) = n \big ( \theta(1 - \theta) \big )}, 請讀者自行展開計算吧, 我實在是懶得算了...

2. "成功" 機率的信賴區間

如果將 T_{n}^{*} 當作 \theta 的某個值 (或者某個點), 那麼就會出現錯誤. 因為對於某些 \omega, 很可能出現 T_{n}^{*}(\omega) 的值對 \theta 的偏差相當大. 因此, 我們還需要對估計的誤差進行衡量.

儘管我們不能指望對於所有基本事件 \omega, T_{n}^{*} = T_{n}^{*}(\omega) 都能與 \theta 的值差異甚小, 這也是毫無意義的. 不過, 通過大數法則, 我們可以知道對於充分大的 n 和任意 \delta > 0, 事件 \left \{ \left | \theta - T_{n}^{*} \right | > \delta \right \} 的機率都充分小.

根據 Chebyshev 不等式 (《【機率論】初等機率論——Bernoulli 概型 : 大數法則》引理 1), 我們有 \displaystyle {\begin {aligned} \mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*} \right | > \delta \right \} &= \mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*} \right |^{2} > \delta \right \} \\ &\leq \frac {\mathop {\mathrm {E}}_{\theta} \left ( (\theta - T_{n}^{*})^{2} \right )}{\delta^{2}} = \frac {\mathop {\mathrm {Var}}_{\theta}(T_{n}^{*})}{\delta^{2}} = \frac {\theta(1 - \theta)}{n\delta^{2}}. \end {aligned}} 對於 \delta = \lambda \sqrt {\frac {\theta(1 - \theta)}{n}}, 有 \displaystyle {\mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*} \right | > \delta \right \} = \mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*}\right | > \lambda \sqrt {\frac {\theta(1 - \theta)}{n}} \right \} \leq \frac {1}{\lambda^{2}}}. 其中, \lambda > 0. 相反地, 我們可以得到 \displaystyle {\mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*} \right | \leq \delta \right \} = \mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*}\right | \leq \lambda \sqrt {\frac {\theta(1 - \theta)}{n}} \right \} \leq 1 - \frac {1}{\lambda^{2}}}. 例如, 取 \lambda = 3, 那麼事件 \left \{ \left | \theta - T_{n}^{*} \right | \leq 3 \sqrt {\frac {\theta(1 - \theta)}{n}} \right \} 出現的機率為 \frac {8}{9}. 特別地, 若 \theta(1 - \theta) \leq \frac {1}{4}, 那麼事件 \left \{ \left | \theta - T_{n}^{*} \right | \leq \frac {3}{2\sqrt {n}} \right \} 出現的機率為 \frac {8}{9}. 我們進行一些變換, \displaystyle {\begin {aligned} \mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*} \right | \leq \frac {3}{2\sqrt {n}} \right \} &= \mathop {\textbf {P}}_{\theta} \left \{ -(\theta - T_{n}^{*}) \leq \frac {3}{2\sqrt {n}} \leq \theta - T_{n}^{*} \right \} \\ &= \mathop {\textbf {P}}_{\theta} \left \{ T_{n}^{*} - \theta \leq \frac {3}{2\sqrt {n}}\ \text {且}\ \frac {3}{2\sqrt {n}} \leq \theta - T_{n}^{*} \right \} \\ &= \mathop {\textbf {P}}_{\theta} \left \{ \theta \geq T_{n}^{*} - \frac {3}{2\sqrt {n}}\ \text {且}\ \theta \leq T_{n}^{*} + \frac {3}{2\sqrt {n}} \right \} \\ &= \mathop {\textbf {P}}_{\theta} \left \{ T_{n}^{*} - \frac {3}{2\sqrt {n}} \leq \theta \leq T_{n}^{*} + \frac {3}{2\sqrt {n}} \right \} \geq \frac {8}{9}. \end {aligned}} 換句話說, 未知參數 \theta 屬於區間 \left [ T_{n}^{*} - \frac {3}{2\sqrt {n}}, T_{n}^{*} + \frac {3}{2\sqrt {n}} \right ] 的機率大於等於 \frac {8}{9}. 有時候, 我們可以記為 \displaystyle {\theta \simeq T_{n}^{*} \pm \frac {3}{2\sqrt {n}} \left (\geq \frac {8}{9} \right )}. 通過上述分析, 我們可以對信賴區間進行定義.

定義 4. 若任意 \theta \in \Theta, 有 \displaystyle {\mathop {\textbf {P}}_{\theta} \left \{ \psi_{1}(\omega) \leq \theta \leq \psi_{2}(\theta) \right \} \geq 1 - \delta} 成立, 那麼稱形如 [\psi_{1}(\omega), \psi_{2}(\omega)] 這樣的區間為可信度為 1 - \delta 的信賴區間或者稱為顯著性水平為 \delta 的信賴區間. 其中, \psi_{1}(\omega) 和 \psi_{2}(\omega) 是關於基本事件 \omega 的兩個函數.

我們在大數法則中就指出, 基於 Chebyshev 不等式的估計是粗略的. 此處同樣是這樣. 我們所得到的 \theta \in \left [ T_{n}^{*} - \frac {\lambda}{2\sqrt {n}}, T_{n}^{*} + \frac {\lambda}{2\sqrt {n}} \right ] 的可信度為 1 - \frac {1}{\lambda^{2}}. 實際上, 可信度要比 1 - \frac {1}{\lambda^{2}} 要高得多.

為了得到更加精確的可信度, 我們注意到 \displaystyle {\left \{ \omega : \left | \theta - T_{n}^{*} \right | \leq \lambda\sqrt {\frac {\theta(1 - \theta)}{n}} \right \} = \left \{ \omega : \psi_{1}(T_{n}^{*}, n) \leq \theta \psi_{2}(T_{n}^{*}, n) \right \}}. 其中, \psi_{1} = \psi_{1}(T_{n}^{*}, n) 和 \psi_{2} = \psi_{2}(T_{n}^{*}, n) 是橢圓方程式 \displaystyle {(\theta - T_{n}^{*})^{2} = \frac {\lambda^{2}}{n}\theta(1 - \theta)\ \ \ \ \ \ \ \ \ \ (\mathrm {IV})} 的根.

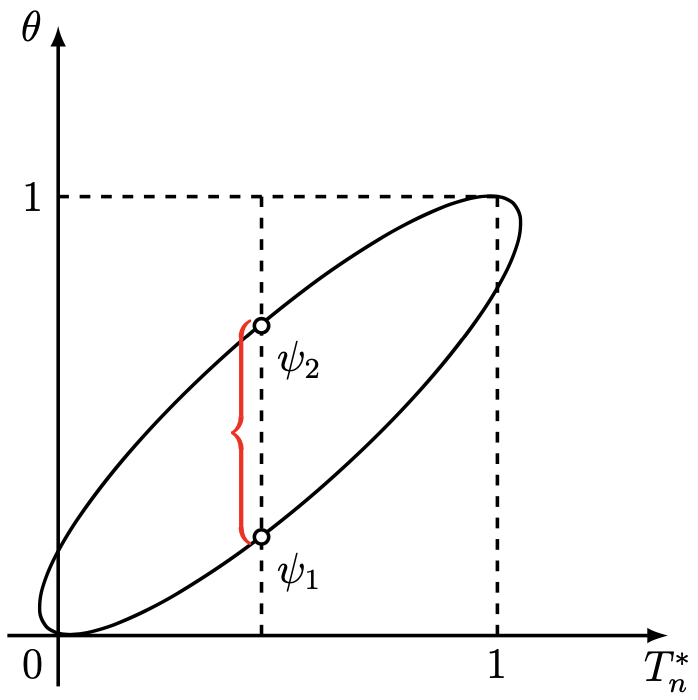
現在記 F_{\theta}^{n}(x) = \mathop {\textbf {P}}_{\theta} \left \{ \frac {S_{n} - n\theta}{\sqrt {n\theta(1 - \theta)}} \leq x \right \}. 我們曾經在《【機率論】初等機率論 – Bernoulli 概型 : 極限定理》中得到 \displaystyle { \sup \limits_{-\infty < x < +\infty} \left | F_{\theta}^{n}(x) - \Phi(x) \right | \leq \frac {\theta^{2} + (1 - \theta)^{2}}{\sqrt {n\theta(1 - \theta)}}}. 其中, \Phi(x) = \frac {1}{\sqrt {2\pi}}\int_{-\infty}^{x}e^{-\frac {t^{2}}{2}}\mathrm {d}t. 由均值不等式, 我們可以得到 \displaystyle {\theta^{2} + (1 - \theta)^{2} = \theta^{2} + \theta^{2} - 2\theta + 1 \leq \theta^{2} + \theta^{2} - (\theta^{2} + \theta^{2}) + 1 = 1}. 因此, 我們有 \displaystyle {\sup \limits_{-\infty < x < +\infty} \left | F_{\theta}^{n}(x) - \Phi(x) \right | \leq \frac {1}{\sqrt {n\theta(1 - \theta)}}}. 如果我們事前已知 0 < \Delta \leq \theta \leq 1 - \Delta < 1, 那麼自然地也有 0 < 1 - \Delta \leq 1 - \theta < \Delta < 1. 其中, \Delta 是某一常數. 那麼 \displaystyle {\frac {1}{\sqrt {n\theta(1 - \theta)}} \leq \frac {1}{\sqrt {n\Delta(1 - \theta)}} \leq \frac {1}{\sqrt {n\Delta \cdot \Delta}} = \frac {1}{\Delta\sqrt {n}}}, 則 \displaystyle {\sup \limits_{-\infty < x < +\infty} \left | F_{\theta}^{n}(x) - \Phi(x) \right | \leq \frac {1}{\Delta\sqrt {n}}}. 從而 \displaystyle {\begin {aligned} \mathop {\textbf {P}}_{\theta} \left \{ \psi_{1}(T_{n}^{*}, n) \leq \theta \leq \psi_{2}(T_{n}^{*}, n) \right \} &= \mathop {\textbf {P}}_{\theta} \left \{ \left | \theta - T_{n}^{*} \right | \leq \lambda \sqrt {\frac {\theta(1 - \theta)}{n}} \right \} \\ &= \mathop {\textbf {P}}_{\theta} \left \{ \frac {\left | S_{n} - n\theta \right |}{\sqrt {n\theta(1 - \theta)}} \leq \lambda \right \} \geq \big ( 2\Phi(\lambda) - 1 \big ) - \frac {2}{\Delta\sqrt {n}}. \end {aligned}} 設 \lambda^{*} 是滿足 \displaystyle {\big ( 2\Phi(\lambda) - 1 \big ) - \frac {2}{\Delta\sqrt {n}} \leq 1 - \delta^{*}} 的最小 \lambda 值, 其中 \delta^{*} 是給定的顯著性水平. 記 \delta = \delta^{*} - \frac {2}{\Delta\sqrt {n}}, 則 \lambda^{*} 是如下方程式的根 : \displaystyle {\Phi(\lambda) = 1 - \frac {\delta}{2}}. 當 n 比較大的時候, 可以忽略項 \frac {2}{\Delta\sqrt {n}}, 於是可以認為 \lambda^{*} 滿足關係式 \displaystyle {\Phi(\lambda^{*}) = 1 - \frac {\delta^{*}}{2}}.

例如, 若 \lambda^{*} = 3, 則 1 - \delta^{*} \doteq 0.9973. 因此以近似的機率 0.9973, 我們有 \displaystyle {T_{n}^{*} - 3 \sqrt {\frac {\theta(1 - \theta)}{n}} \leq \theta \leq T_{n}^{*} + 3\sqrt {\frac {\theta(1 - \theta)}{n}}}. 更進一步地, 經過迭代並且忽略量級為 O(n^{-\frac {3}{4}}) 的項, 得到 \displaystyle {T_{n}^{*} - 3 \sqrt {\frac {T_{n}^{*}(1 - T_{n}^{*})}{n}} \leq \theta \leq T_{n}^{*} + 3\sqrt {\frac {T_{n}^{*}(1 - T_{n}^{*})}{n}}}. 由此可見, 對於充分大的 n, 可信區間 \left [ T_{n}^{*} - \frac {3}{2\sqrt {n}}, T_{n}^{*} + \frac {3}{2\sqrt {n}} \right ] 的可信度高達 0.9973, 比通過 Chebyshev 不等式得到的可信度要高出近 11\%.

由此可見, 加入進行大量 N-系列試驗, 每系列試驗根據 n 次觀測的結果估計參數 \theta. 那麼平均情況下, 有 99.73\% 的機率, 估計量和參數 \theta 的差值不大於 \frac {3}{2\sqrt {n}}.