考察一個程式的作業計數和程式步伐主要有兩個原因 :

1. 預測程式運作的時間如何隨著實體特徵的變化而變化
2. 對兩個相同功能的演算法, 比較它們的時間複雜度

在使用作業計數的時候, 我們通常選擇我們感興趣的部分而暫時忽略了其它因素. 因此, 這種方法在選擇的時候, 應該儘量謹慎

作業計數說明的僅僅是一個程式的部分工作, 而程式步伐要說明所有工作. 但是由於程式步伐沒有精確定義, 陳述式 x = y 以及 x = y + z / x % y 都可以算作是一個程式步伐. 於是, 對於同樣的程式, 不同的分析員所計算得到的程式步伐存在差異. 例如某一個分析員對於 for(auto i {0}; i < n; ++i) 這樣的迴圈, 他並不將 i 的初始化計入程式步伐. 因此, 由於程式步伐的定義不嚴謹, 不同的人得到的程式步伐在比較程式性能方面的用處並不大. 但是對於同一個人計算而得的程式步伐相差很大的程式碼, 如某個程式步伐為 an + b (a > 0), 另一個程式步伐為 cn + d (c \gg d), 那麼此事可以使用程式步伐來判定程式的性能

當實體特徵 n 非常大 (n \rightarrow \infty) 的時候, 此時使用程式步伐可以準確地預計程式的運作時間的增長, 以比較兩個程式的性能. 若某個程式的程式步伐為 c_{1}n^{2} + c_{2}n + c_{3} (c_{1} > 0), 另一個程式的程式步伐為 c_{4}n + c_{5} (c_{4} > 0). 當 n 充分大的時候, 第一個程式的程式步伐會比第二個程式的程式步伐大得多 :

\lim \limits_{n \to \infty} \frac {c_{1}n^{2}+c_{2}n+c_{3}}{c_{4}n+c_{5}} = \infty

對程式步伐為 c_{1}n^{2} + c_{2}n + c_{3} (c_{1} > 0) 的程式, 若不考慮 c_{1}, c_{2} 和 c_{3} 的具體值, 我們發現, 當 n 增大的時候, 整個表達式的值最終取決於第一項 c_{1}n^{2} 作比率函數 :

R(n) = \frac {c_{2}n + c_{3}}{c_{1}n^{2}}

當 n 充分大的時候, 雖然 R(n) 不會等於 0, 但是會無限接近與 0. 即當 n \to \infty 時, 有 R(n) \to 0. 因此, 當 n 充分大, c_{2}n + c_{3} 與 c_{1}n^{2} 相比, 其大小無關緊要. 因此, 一個程式的運作時間可以近似得使用 c_{1}n^{2} 來表示

設 n_{1} 和 n_{2} 是兩個關於 n 的兩個很大的值, 記 t(n) = c_{1}n^{2} + c_{2}n + c_{3}, 令 T = \frac {t(n_{1})}{t(n_{2})}, 則有

T = \frac {t(n_{1})}{t(n_{2})} = \frac {c_{1}n_{1}^{2}+c_{2}n_{1}+c_{3}}{c_{1}n_{2}^{2}+c_{2}n_{2}+c_{3}}

由於 n_{1} 和 n_{2} 足夠大, 因此有

T \doteq  \frac {c_{1}n_{1}^{2}}{c_{1}n_{2}^{2}} = (\frac {n_{1}}{n_{2}})^{2}

若 n_{1} = 2n, n_{2} = n, 則有

T = 4

即當實體特徵增大 2 倍的時候, 程式運作時間近似地增大到原來的 4 倍. 類似地, 令 n_{2} 保持不變, n_{1} = 3n, 則 T = 9; ...

於是我們認識到只要知道程式步伐的最大項為 n^{2} 就可以了, 其係數 c_{1} 無關緊要

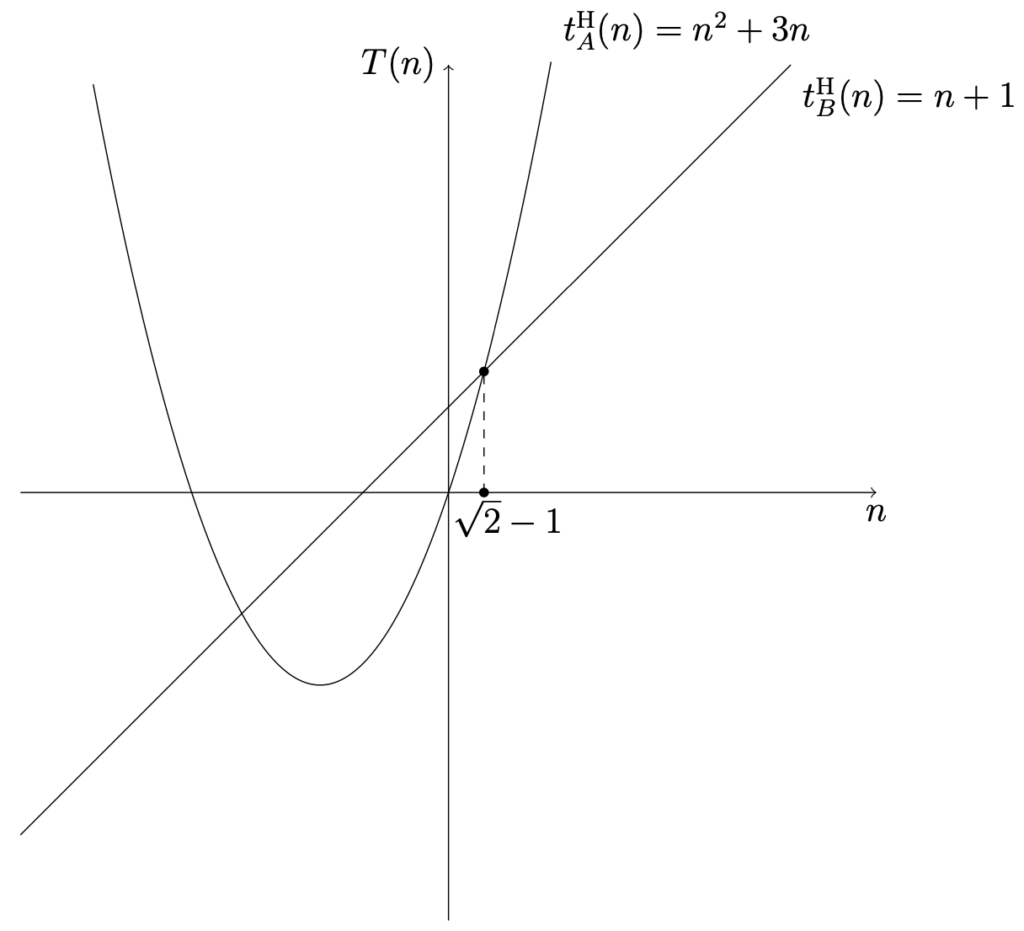
假定程式 A 和程式 B 具有相同的功能, 有兩個人 H 和 W 對這兩個程式進行了步伐分析. H 對程式 A 分析後得到程式 A 的程式步伐滿足 t_{A}^{H}(n) = n^{2} + 3n, 對程式 B 分析後得到的結果為 t_{B}^{H}(n) = 32n; W 對程式 A 分析後得到程式 A 的程式步伐滿足 t_{A}^{W}(n) = 2n^{2} + 6n, 對程式 B 分析後得到的結果為 t_{B}^{W}(n) = 48n. 如果 H 的分析是正確的, 那麼任何人的分析結果想要正確, 其必須滿足

t_{A}(n) = c_{1}n^{2} + c_{2}n + c_{3} (c_{1} > 0), t_{B}(n) = c_{4}n + c_{5} (c_{4} > 0)

的結果. 其中, c_{1}, c_{2}, c_{3}, c_{4} 和 c_{5} 為任意常數

顯然, 針對 H 的分析結果和 W 的分析結果, t = t_{A}^{H}(n) 和 t = t_{B}^{H}(n) 是兩條不同的曲線, t = t_{A}^{W}(n) 和 t = t_{B}^{W}(n) 也是兩條不同的曲線

對於 H 的分析結果, 它們有共同的交點, 即當 n = 0 和 n = 29 時, t_{A}^{H}(n) = t_{B}^{H}(n), 稱這樣的 n 為程式的均衡點. 當 n = 0 的時候, 無需分析; 當 0 < n < 29 時, 程式 A 更快; 當 n > 29 的時候, 程式 B 更快

再來看看 W 的分析結果

其均衡點為 n = 0 或 n = 21. 當 n = 0 的時候, 無需分析; 當 0 < n < 21 時, 程式 A 更快; 當 n > 21 時, 程式 B 更快

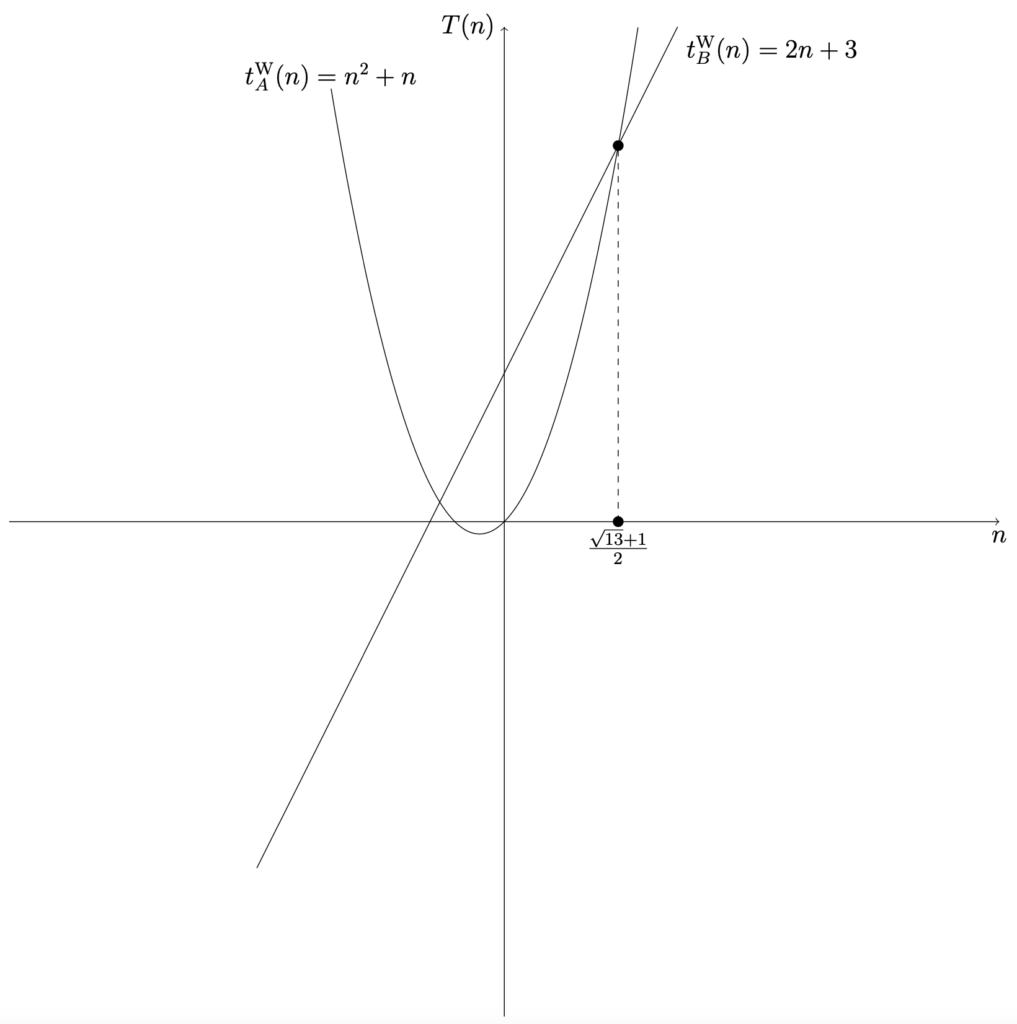
最終, 不論 t_{A}(n) 與 t_{B}(n) 的結果如何, 只要分析正確, 必定有一個非零的均衡點. 此時, 我們會得到當 n 位於均衡點左側的時候, 程式 A 更快; 當 n 位於均衡點右側的時候, 程式 B 更快的結論, 無非是均衡點不同罷了. 為此, 有了漸近分析

漸近分析方法主要確定的是針對複雜函數中的最大項, 即針對當 n 充分大的時候, 最終決定函數值大小的那一項進行分析. 漸近分析是數學分析的一個分支, 它是數學分析中描述函數在極限附近的行為的方法

令 p(n) 和 q(n) 是兩個非負值函數, 若且唯若

\lim \limits_{n \to \infty} \frac {q(n)}{p(n)} = 0 或 \lim \limits_{n \to \infty} \frac {p(n)}{q(n)} = \infty

時, 稱 p(n) 漸近地大於 q(n), q(n) 漸近地小於 p(n); 若且唯若

\lim \limits_{n \to \infty} \frac {p(n)}{q(n)} = 0 或 \lim \limits_{n \to \infty} \frac {q(n)}{p(n)} = \infty

時, 稱 q(n) 漸近地大於 p(n), p(n) 漸近地小於 q(n); 若且唯若

\lim \limits_{n \to \infty} \frac {p(n)}{q(n)} = \lim \limits_{n \to \infty} \frac {q(n)}{p(n)} = 1

時, 稱 q(n) 漸近地等於 p(n), p(n) 漸近地等於 q(n)

在接下來的討論中, 函數 f(n) 和 g(n) 等都是作為實體特徵 n 的函數, 表示一個程式的空間複雜度或時間複雜度. 因為程式的空間複雜度或時間複雜度都是非負數, 實體特徵也是非負數, 因此對於任意非負的 n, 我們都假定函數 f 對實體特徵 n 有非負值, 即

f(n) \geq 0 (n \geq 0)

我們給定經常在步伐分析中出現的項

要注意, 給定的項係數都為 1, 但是在實際分析中, 它們的係數不一定為 1, 可能具有不同的值. 特別指出, 對於對數, 不妨設其底數為 a, 而

\log_{a} n = \log_{a} b \cdot \log_{b} n (a > 1, b > 1)

因此, 在步伐分析中, 係數通常會被省略. 因此, 任意底數 a 的對數 (a > 1) 是漸近相等的

根據增長的趨勢, 我們容易地得到這些項的大小排列 :

1 < \log n < n < n\log n < n^{2} < n^{2}\log n < n^{3} < 2^{n} < n!

其中, "<" 表示漸近小於

漸近記法描述的是大實體特徵的時間複雜度, 我們將用它來分析程式步伐. 除此之外, 它還可以被用於分析空間複雜度和作業計數. 時間複雜度和程式步伐是同義詞. 如果實體特徵只含有一個變數, 如 n, 漸近記法就用程式步伐中漸近最大的一項來描述複雜度

漸近記法 f(n) = O(g(n)) 表示函數 f(n) 漸近小於或等於函數 g(n), 即

\lim \limits_{n \to \infty} \frac {f(n)}{g(n)} = 0 或 \lim \limits_{n \to \infty} \frac {f(n)}{g(n)} = \lim \limits_{n \to \infty} \frac {g(n)}{f(n)} = 1

稱這樣的漸近記法為大 O 記法. 在漸近的意義上, 函數 g(n) 是函數 f(n) 的上限. 需要指出的是, 此處的大 O 記法的定義並非嚴格定義, 而是實用定義

對於 f(n) = O(g(n)), 除了函數 f(n) = 0 以外, 函數 g(n) 習慣上是一個單位項, 即一個係數為 1 的單項, 而且通常是令 f(n) = O(g(n)) 能夠成立的最小單位項. 當 f(n) = 0 時, g(n) = 0

在漸近分析中, 我們要確定一個最大項以表示複雜度, 而且把這個最大項的係數置為 1. 例如對於函數

f(n) = 3n^{3} + 4n^{2} + 8n\log_{3} n + 6n + 5\log_{2} n + 4

的單位項分別是 n^{3}, n^{2}, n\log n, n, \log n 和 1. 若一個程式的程式步伐滿足函數 f(n), 則其漸近複雜度為 O(n^{3})

另外, f(n) = O(g(n)) 與 O(g(n)) = f(n) 不同. 實際上, 後者沒有任何意義. 等號在此處表示的 "是" 的含義, 而非表面上相等的含義. 將 f(n) = O(g(n)) 翻譯為英文, 讀作 f(n) is big oh of g(n)

當某個程式與兩個實體特徵相關的時候, 令 t(m, n) 和 u(m, n) 為兩項, 若且唯若

\lim \limits_{n \to \infty} \frac {u(m, n)}{t(m, n)} = 0 且 \lim \limits_{m \to \infty} \frac {u(m, n)}{t(m, n)} \neq \infty

或

\lim \limits_{n \to \infty} \frac {u(m, n)}{t(m, n)} \neq \infty 且 \lim \limits_{m \to \infty} \frac {u(m, n)}{t(m, n)} = 0

則稱 t(m, n) 漸近地大於 u(m, n), u(m, n) 漸近地小於 t(m, n)

對於多元的程序步伐函數, 大 O 記法的實用定義如下 :

• 令 f(x_{1}, x_{2}, ..., x_{n}) 是一個程式的程式步伐, 其中任一項若漸近小於剩餘的項, 那麼都可以將其去除
• 把最終剩下的項的係數更改為 1

例如 f(m, n) = m^{3} + 3m^{2}n + 10mn + 2n^{2}, 那麼 f(m, n) = O(m^{3} + m^{2}n + n^{2})

除了大 O 記法之外, 還有大 Ω 記法、大 Θ 記法和小 o 記法. 若 f(n) 漸近地大於或等於 g(n), 則記作 f(n) = \Theta(g(n)); 若 f(n) 漸近地等於 g(n), 則記作 f(n) = \Omega(g(n)); 若 f(n) 漸近地大於 g(n), 即當 f(n) = O(g(n)) 且 f(n) \neq \Omega(g(n)), 則記作 f(n) = o(g(n))

大 O 記法和大 Θ 記法比較常用, 而大 Ω 記法不是很常用, 小 o 記法在資料結構的漸近分析中非常少見, 不過在數學分析中很常見

從漸近分析的意義上來說, 若有 f(n) = O(g(n)), 則函數 g(n) 是函數 f(n) 的上界; 若有f(n) = \Omega(g(n)), 則函數 g(n) 是函數 f(n) 的下界. 若有 f(n) = \Theta(g(n)), 那麼稱函數 f(n) 有界, 即函數 f(n) 既有上界, 也有下界

有時候, 我們會遇到單個的 O(g(n)), \Theta(g(n)) 和 \Omega(g(n)), 那麼可以將其視為一個集合 :

O(g(n)) = \left \{ f(n) : f(n) = O(g(n)) \right \}

\Theta(g(n)) = \left \{ f(n) : f(n) = \Theta(g(n)) \right \}

\Omega(g(n)) = \left \{ f(n) : f(n) = \Omega(g(n)) \right \}

基於這種解釋, 於是有類似於

O(g_{1}(n)) = O(g_{2}(n))

的表示方法

之前, 我們大致講述了大 O 記法、大 Ω 記法和大 Θ 記法的實用定義. 接著, 我們需要給出它們的精確定義, 否則, 某些定理或著結論我們沒有辦法去證明. 值得注意的是, 小 o 記法的定義可以由大 O 記法、大 Ω 記法和大 Θ 記法的定義推出, 因此之前我們對小 o 記法的定義已經是一個精確定義, 只不過我們需要補充大 O 記法、大 Ω 記法和大 Θ 記法的精確定義才能使的小 o 記法的定義精確

提示 : 如果你了解數學分析中的極限理論, 那麼接下來的內容對你來說非常容易掌握. 但是如果你沒有了解過極限理論, 那麼接下來你的學習可能有些吃力. 目前 Jonny'Blog 已經開通了數學 - 分析學欄目, 閣下可以去搜尋關於極限理論的文章, 此處不再對極限理論進行累贅. 如果你以後要學習極限理論, 而你又能夠理解下面的內容, 那麼這對於你以後學習極限理論非常有幫助

定義 1 (大 O 記法) : 對於函數 f(n) 和 g(n), 若且唯若存在常數 c > 0 和正整數 N, 使得對於所有的 n \geq N 都有

f(n) \leq cg(n)

成立時, 記 f(n) = O(g(n))

當 n \geq N 時, 有 f(n) \leq cg(n) 成立, 這說明當 n 充分大的時候, cg(n) 是 f(n) 的一個上界. 任取正整數 N, 函數值 f(n) 可能大於、小於或等於函數值 cg(n), 但是一定存在一個正整數 N_{0}, 當 n \geq N_{0} 時, f(n) 的函數值永遠不會大於 cg(n) 的函數值

函數 g 作為函數 f 的一個上界, 形式通常比較簡單. 一般只是用一個變數 n 表示且係數為 1 的單項

有了大 O 記法的嚴格定義, 我們可以證明某些斷言 :

斷言 : f(n) = 3n^{2}2^{n} + 4n2^{n} + 8n^{2} \neq O(2^{n})

證明 :

我們使用歸謬法進行證明. 不妨設 f(n) = 3n^{2}2^{n} + 4n2^{n} + 8n^{2} = O(2^{n}), 根據大 O 記法的定義, 存在某個常數 c > 0 和一個正整數 N, 當 n \geq N 的時候, 有

f(n) \leq c \cdot 2^{n}

即

3n^{2}2_{n} + 4n2^{n} + 8n^{2} \leq c \cdot 2^{n}

不等式兩側同乘 \frac {1}{2^{n}}, 可得

3n^{2} + 4n + \frac {8n^{2}}{2^{n}} \leq c

令 g(x) = 3x^{2} + 4x + \frac {8x^{2}}{2^{x}}, 則 g'(x) = 6x + 4 + 2^{3-x}x(2 - \ln 2x)

令 g'(x) = 0, 可知使得 g(x) = 0 的點 x = x_{0} < 0. 而 g(0) > 0, 則 g(x) 在 (0, + \infty) 上單調增加. 故對於任意 n > 0, g(n) 單調增加. 由於 c 是常數, 因此 3n^{2} + 4n + \frac {8n^{2}}{2^{n}} \leq c 僅在有限處成立. 因此假設不成立

綜上所述, f(n) = 3n^{2}2_{n} + 4n2^{n} + 8n^{2} \neq O(2^{n})

證畢

事實上, f(n) = 3n^{2}2^{n} + 4n2^{n} + 8n^{2} = O(n^{2}2^{n}) f(n) = O(g(n)) 表明存在一個常數 c > 0 和正整數 N, 當 n \geq N 時, cg(n) 是 f(n) 的上限, 並未表明這個上限是否為 f(n) 的最小上限 (即上確界). 因此為了使得 f(n) = O(g(n)) 有實際意義, g(n) 應該儘量小

根據大 O 記法的嚴格定義, 我們可以得到兩個定理

大 O 記法定理 1 : 如果 f(n) = a_{m}n^{m} + a_{m - 1}n^{m - 1} + ... + a_{1}n + a_{0}, 其中 a_{m} > 0, 那麼 f(n) = O(n^{m})

證明 :

首先, 我們注意到 n \geq 1, 於是我們注意到不等式

f(n) \leq \sum \limits_{i = 0}^{m} |a_{i}| n^{i} \leq n^{m} \sum \limits_{i = 0}^{m} |a_{i}| n^{i - m} \leq n^{m} \sum \limits_{i = 0}^{m} |a_{i}|

根據大 O 記法的定義, 因此有 f(n) = O(n^{m})

證畢

大 O 記法定理 2 (大 O 記法比率定理) : 假設函數 f = f(n), g = g(n) 滿足極限

\lim \limits_{n \to \infty} \frac {f(n)}{g(n)}

存在, 若且唯若存在常數 c 使得

\lim \limits_{n \to \infty} \frac {f(n)}{g(n)} \leq c

時, 有 f(n) = O(g(n))

證明 :

要證明這個定理成立, 其實就是要證明使得 f(n) = O(g(n)) 成立的充分必要條件是存在常數 c, 使得

\lim \limits_{n \to \infty} \frac {f(n)}{g(n)} \leq c

若有 f(n) = O(g(n)) 成立, 則根據大 O 記法的定義, 存在常數 c > 0 和正整數 N, 當 n \geq N 時, 有

f(n) \leq cg(n)

即 \frac {f(n)}{g(n)} \leq c, 亦即 \lim \limits_{n \to \infty} \frac {f(n)}{g(n)} \leq c

充分性證畢

若 \lim \limits_{n \to \infty} \frac {f(n)}{g(n)} \leq c 成立, 根據數列極限的定義, 存在正整數 N, 當 n \geq N 時, 有

|\frac {f(n)}{g(n)} - c_{0}| \leq \varepsilon

其中, \lim \limits_{n \to \infty} \frac{f(n)}{g(n)} = c_{0} \leq c, \varepsilon > 0. 則有

-\varepsilon + c_{0} \leq \frac {f(n)}{g(n)} \leq \varepsilon + c_{0}

即 f(n) \leq (\varepsilon + c_{0})g(n)

取 c = \max \left \{ 1, \varepsilon + c_{0} \right \}, 於是有 f(n) \leq cg(n) 成立

必要性證畢

綜上所述, f(n) = O(g(n)) 成立的充分必要條件是存在常數 c, 使得

\lim \limits_{n \to \infty} \frac {f(n)}{g(n)} \leq c

證畢

使用這個定理, 我們可以很快地得到 g(n). 例如有函數 f(n) = c_{1}n^{2} + c_{2}n + c_{3}, 其中 c_{1} > 0, 由於

\lim \limits_{n \to \infty} \frac {c_{1}n^{2} + c_{2}n + c_{3}}{n^{2}} = c_{1}

任取 c (c \geq c_{1}), 有 f(n) \leq c_{1}n^{2}. 因此, 由大 O 記法比率定理可知

f(n) = O(n^{2})

定義 2 (大 Ω 記法) : 對於函數 f(n) 和 g(n), 若且唯若存在常數 c > 0 和正整數 N, 使得對於所有的 n \geq N 都有

f(n) \geq cg(n)

成立時, 記 f(n) = \Omega(g(n))

大 Ω 記法也簡稱 Ω 記法

Ω 記法定理 1 : 如果 f(n) = a_{m}n^{m} + a_{m - 1}n^{m - 1} + ... + a_{1}n + a_{0}, 其中 a_{m} > 0, 那麼 f(n) = \Omega(n^{m})

證明 :

我們通過不斷縮小 f(n), 可以觀察到

f(n) = a_{m}n^{m} + a_{m - 1}n^{m - 1} + ... + a_{1}n + a_{0} \geq a_{m}n^{m} + a_{m - 1}n^{m - 1} + ... + a_{1}n \geq a_{m}n^{m} + a_{m - 1}n^{m - 1} + ... + a_{2}n^{2} \geq ... \geq a_{m}n^{m} + a_{m - 1}n^{m - 1} \geq a_{m}n^{m}

根據 Ω 記法的定義, 有

f(n) = \Omega(n^{m})

證畢

Ω 記法定理 2 (O 記法比率定理) : 假設函數 f = f(n), g = g(n) 滿足極限

\lim \limits_{n \to \infty} \frac {f(n)}{g(n)}

存在, 若且唯若存在常數 c 使得

\lim \limits_{n \to \infty} \frac {g(n)}{f(n)} \leq c

時, 有 f(n) = \Omega(g(n))

這個定理的證明和大 O 記法比率定理的證明相同, 此處我們不再重複證明, 閣下也可以自己嘗試證明這個定理

定義 3 (大 Θ 記法) : 對於函數 f(n) 和 g(n), 若且唯若存在常數 c_{1} > 0, c_{2} > 0 和正整數 N, 使得對於所有的 n \geq N 都有

c_{1}g(n) \geq f(n) \geq c_{2}g(n)

成立時, 記 f(n) = \Theta(g(n))

大 Θ 記法也簡稱 Θ 記法

Θ 記法定理 1 : 如果 f(n) = a_{m}n^{m} + a_{m - 1}n^{m - 1} + ... + a_{1}n + a_{0}, 其中 a_{m} > 0, 那麼 f(n) = \Theta(n^{m})

證明 :

由大 O 記法定理 1 和大 Ω 記法定理 1 的證明可知 :

a_{m}n^{m} \leq f(n) \leq n^{m} \sum \limits_{i = 0}^{m} |a_{i}|

取 c_{1} = a_{m}, c_{2} = \sum \limits_{i = 0}^{m} |a_{i}|, 根據大 Θ 記法的定義, 有 f(n) = \Theta(n^{m})

證畢

Θ 記法定理 2 (Θ 記法比率定理) : 假設函數 f = f(n), g = g(n) 滿足極限

\lim \limits_{n \to \infty} \frac {f(n)}{g(n)} 及 \lim \limits_{n \to \infty} \frac {g(n)}{f(n)}

存在, 若且唯若存在常數 c 使得

\lim \limits_{n \to \infty} \frac {g(n)}{f(n)} \leq c 且 \lim \limits_{n \to \infty} \frac {f(n)}{g(n)} \leq c

時, 有 f(n) = \Theta(g(n))

結合大 O 記法比率定理和 Ω 記法比率定理就可以得證 Θ 記法比率定理, 因此這個定理我們不證, 閣下可以自己嘗試證明

通過對 Θ 記法定理 1 和 Θ 記法比率定理的分析, 我們可以得到關於 Θ 記法的另外一種定義 :

定義 3' (大 Θ 記法) : 對於函數 f(n) 和 g(n), 若有 f(n) = O(g(n)) 與 f(n) = \Omega(g(n)) 同時成立, 則記 f(n) = \Theta(g(n))

定義 4 (小 o 記法) : 對於函數 f(n) 和 g(n), 若有 f(n) = O(g(n)) 與 f(n) \neq \Omega(g(n)) 同時成立, 則記f(n) = o(g(n))

小 o 記法經常用於步伐函數的分析. 在步伐函數的分析中, 小於 \Theta(n) 的部分通常可以忽略不計. 例如函數 f(n) = c_{1}n^{2} + c_{2}n + c_{3}, 其中 c_{1} > 0, 可以將 f(n) 記為 f(n) = c_{1}n^{2} + o(n^{2}). 在數學分析中, 有一個定義和小 o 記法非常相似, 即高階無窮小

我們曾經說過, 大 O 記法和 Θ 記法比較常用, 而 Ω 記法不是很常用. 現在我們有了它們的精確定義, 來闡述一下得到這個斷言的原因. 大 O 記法實際上是程式步伐函數的上界, 也就是說若有 f(n) = O(g(n)), 那麼程式運作時間不會大於 cg(n); Ω 記法是程式步伐函數的下界, 也就是說若有 f(n) = \Omega(g(n)), 那麼程式運作時間不小於 cg(n); Θ 記法式程式步伐函數的確界, 也就說若有 f(n) = \Theta(g(n)), 那麼程式的運作時間會介於 c_{1}g(n) 和 c_{2}g(n) 之間. 其中, c > 0, c_{2} > c_{1} > 0, c, c_{1}, c_{2} 為任意常數. 對於任意演算法來說, 我們非常自然地就會限制演算法的運作時間的上界, 因為我們不希望演算法用時過長, 也就是複雜度過高. 然而, 我們幾乎不會關心一個演算法的運作時間的下界, 因為這幾乎沒什麼用. 因此, 大 O 記法比 Ω 記法要常用得多. 但是, 我們為什麼又會說 Θ 記法也比較常用呢? 這是因為對於很多演算法, 我們確實可以證明它的步伐函數存在下界, 與其模模糊糊地使用大 O 記法描述, 倒不如 Θ 記法更精確一些. 這就是為什麼有些人更喜歡 Θ 記法的原因. 但是, 要想要精確, 我們就必須證明步伐函數的下界存在, 大部分人不喜歡過多的證明, 因此大 O 記法會比 Θ 記法用得多一些. 一般來說, 如果我們證明了某個步伐函數的上界確實存在, 順手證明了步伐函數也存在下界, 此時就會使用 Θ 記法; 否則, 我們更多地使用大 O 記法

任取 \varepsilon > 0, 令 x > 0, 下面結論均成立 :

1. 存在正整數 N, 當 n \geq N 時, 有 (\log n)x < (\log n)^{x + \varepsilon}
2. 存在正整數 N, 當 n \geq N 時, 有 (\log n)x <n^{\varepsilon}
3. 存在正整數 N, 當 n \geq N 時, 有 n^{x} < n^{x + \varepsilon}
4. 存在正整數 N, 當 n \geq N 時, 有 n^{x} < 2^{n}
5. 對於任意實數 y, 存在正整數 N, 當 n \geq N 時, 有 n^{x} (\log n)^{y} < n^{x + \varepsilon}

使用函數的單調性就可以證明上述結論, 此處不再證明

我們已經將大 O 記法的定義推廣到了多元函數, 對於 Ω 記法、Θ 記法和小 o 記法同樣可以推廣到多元函數

對於某些函數 f(n), 我們直接給出漸近分析中的某些結論 :

• f(n) = c \Rightarrow f(n) = \bigoplus(1)
• f(n) = \sum \limits_{i = 0}^{k} c_{i}n^{i} \Rightarrow f(n) = \bigoplus(n^{k})
• f(n) = \sum \limits_{i = 0}^{n} i \Rightarrow f(n) = \bigoplus(n^{2})
• f(n) = \sum \limits_{i = 0}^{n} i^{2} \Rightarrow f(n) = \bigoplus(n^{3})
• f(n) = \sum \limits_{i = 0}^{n} i^{k} (k > 0) \Rightarrow f(n) = \bigoplus(n^{k + 1})
• f(n) = \sum \limits_{i = 0}^{n} r^{i} (r > 1) \Rightarrow f(n) = \bigoplus(r^{n})
• f(n) = \sum \limits_{i = 0}^{n} \frac {1}{i} \Rightarrow f(n) = \bigoplus(\log n)
• f(n) = n! \Rightarrow f(n) = \bigoplus(\sqrt {n} (\frac {n}{e})^{n})
• f(n) = \bigoplus(g(n)) \Rightarrow \sum \limits_{n = a}^{b} f(n) = \bigoplus(\sum \limits_{n = a}^{b}g(n))
• f_{i}(n) = \bigoplus(g(n)) (1 \leq i \leq k) \Rightarrow \sum \limits_{i = 1}^{k}f_{i}(n) = \bigoplus(\max \limits_{1 \leq i \leq k}{g_{i}(n)})
• f_{i}(n) = \bigoplus(g(n)) (1 \leq i \leq k) \Rightarrow \prod \limits_{i = 1}^{k}f_{i}(n) = \bigoplus(\prod \limits_{i = 1}^{k}{g_{i}(n)})
• f_{1}(n) = O(g_{1}(n)), f_{2}(n) = \Theta(g_{2}(n)) \Rightarrow f_{1}(n) + f_{2}(n) = O(g_{1}(n) + g_{2}(n))
• f_{1}(n) = \Theta(g_{1}(n)), f_{2}(n) = \Omega(g_{2}(n)) \Rightarrow f_{1}(n) + f_{2}(n) = \Omega(g_{1}(n) + g_{2}(n))
• f_{1}(n) = O(g(n)), f_{2}(n) = \Theta(g(n)) \Rightarrow f_{1}(n) + f_{2}(n) = \Theta(g(n))

其中, c > 0, c_{1} > 0, k 與 r 為正整數, c, c_{1}, c_{2}, ..., c_{n} 為任意常數, \bigoplus 表示 O、\Omega 和 \Theta 中的任意一個

對於複雜度的應用, 前面已經說過了其中一種用法, 即在函式的功能相同的情況下, 我們通常使用複雜度較小的函式. 對於複雜度較小的這個描述, 用 n 充分大更合適. 若程式 P 的時間複雜度為 \Theta(n), 而程式 Q 的時間複雜度為 \Theta(n^{2}), 那麼可以斷定, 若 n 充分大, 那麼程式 P 的速度快於程式 Q. 而 n 充分大, 是可以使用實際數字來表示的. 比如程式 P 的程式步伐函數為 P(n) = 6n + 1, 程式 Q 的程式步伐函數為 Q(n) = n^{2} + 2, 那麼令

Q(n) > P(n), 即 n^{2} + 2 > 6n + 1

解得 n < -2\sqrt {2} + 3, n > 2\sqrt {2} + 3, 由於 -2\sqrt {2} + 3 < 1, 因此這個解可以不必考慮. 大於 2\sqrt {2} + 3 的整數有很多, 任取一個作為 N, 當實體特徵 n > N 時, 程式 P 的速度更快. 但是如果 n \in \{ 1, 2, 3, 4, 5 \} 時, 程式 Q 速度更快

另外, 如果一個程式的時間複雜度是次數較高的多項式級別、指數級別甚至階乘級別, 那麼隨著實體特徵 n 的增大, 那麼程式的程式步伐 (或者說程式的運作時間) 的增加速度會非常快, 最終導致程式運作緩慢. 因此, 在這樣的情況下, 我們應該儘量控制實體特徵 n 或著限制程式的使用. 如果存在時間複雜度較低的演算法, 我們需要重新改寫這個程式

漸近分析僅針對足夠大的 n 給出了程式的時間複雜度. 當 n 比較小的時候, 程式的運作時間可能不足以滿足漸近曲線. 為了確定漸近曲線以外的點, 我們需要檢查若干個 n 值所對應的運作時間, 此時就需要對程式步伐進行分析