摘要訊息 : 一些初等機率論中的經典模型和分佈.

0. 前言

在《【機率論】初等機率論——有限種結局試驗的機率模型》中, 我們對有限種結局試驗建立了機率論體系. 在本節中, 我們將要討論一些經典的機率模型和分佈.

更新紀錄 :

• 2022 年 6 月 6 日進行第一次更新和修正.

1. 二項分佈

假設將一枚硬幣接連擲 n 次, 觀測結果用有序陣列 (a_{1}, a_{2}, ..., a_{n}) 表示. 其中, 當第 i 次擲出現正面時, a_{i} = 1; 當第 i 次擲出現反面時, a_{i} = 0, i = 1, 2, ..., n. 那麼基本事件空間具有如下形式 : \displaystyle {\Omega = \{ \omega : \omega = (a_{1}, a_{2}, ..., a_{n}), a_{i} = 0 \text { 或者 } a_{i} = 1\ (i = 1, 2, ..., n) \}}. 賦予每一個基本事件 \omega = (a_{1}, a_{2}, ..., a_{n}) 以機率 \displaystyle {p(\omega) = p^{\sum \limits_{i : \left \{ a_{i} = 1 \right \}}a_{i}} \cdot q^{n - \sum \limits_{i : \left \{ a_{i} = 1 \right \}}a_{i}}}, 其中 p 與 q 為非負實數且 p + q = 1. 首先, 我們需要說明這樣去定義機率 p(\omega) 的合理性. 為此, 我們只需要驗證 \displaystyle {\sum \limits_{\omega \in \Omega}p(\omega) = 1}.

考慮所有滿足 \displaystyle {\sum \limits_{i\ :\ \{ a_{i} = 1 \}}a_{i} = k} 的基本事件 \omega = (a_{1}, a_{2}, ..., a_{n}). 其中, k = 0, 1, 2, ..., n. 這等同於將 k 個 1 分配至 n 個位置上, 屬於不放回無序抽樣. 因此, 對於任意的正整數 k\ (0 \leq k \leq n), 這樣的基本事件個數共有 \binom {k}{n}. 於是, \displaystyle {\begin {aligned} \sum \limits_{\omega \in \Omega}p(\omega) &= \sum \limits_{k = 0}^{n} \binom {k}{n}p^{k}q^{n - k} \\ &= \binom {0}{n}p^{0}q^{n} + \binom {1}{n}p^{1}q^{n - 1} + ... + \binom {n - 1}{n}p^{n - 1}q^{1} + \binom {n}{n}p^{n}q^{0} \\ &= q^{n} + npq^{n - 1} + ... + np^{n - 1}q + p^{n} \\ &= (p + q)^{n} \\ &= 1^{n} = 1. \end {aligned}} 設 \mathscr {A} 為空間 \Omega 的一切子集的代數, 在 \mathscr {A} 上定義了機率 \displaystyle {\mathop {\mathbf {P}}(A) = \sum \limits_{\omega \in \Omega}p(\omega), A \in \mathscr {A}}. 其中, p(\{ \omega \}) = p(\omega), \omega \in \Omega. 這樣, 我們就定義了描繪 n 次擲硬幣的機率模型.

事件 \displaystyle {A_{k} = \{ \omega : \omega = (a_{1}, a_{2}, ..., a_{n}), a_{1} + a_{2} + ... + a_{n} = k \}} 表示恰好有 k 次 "成功". 其中, k = 1, 2, ..., n. 由之前的討論, 我們知道 \mathop {\mathbf {P}}(A_{k}) = \binom {k}{n}p^{k}q^{n - k} 且 \sum \limits_{k = 0}^{n}\mathop {\mathbf {P}}(A_{k}) = 1. 機率組 (\mathop {\mathbf {P}}(A_{0}), \mathop {\mathbf {P}}(A_{1}), \mathop {\mathbf {P}}(A_{2}), ..., \mathop {\mathbf {P}}(A_{n})) 稱作二項分佈 (binomial distribution), 也稱在容量為 n 的樣本中, "成功" 的次數服從二項分佈.

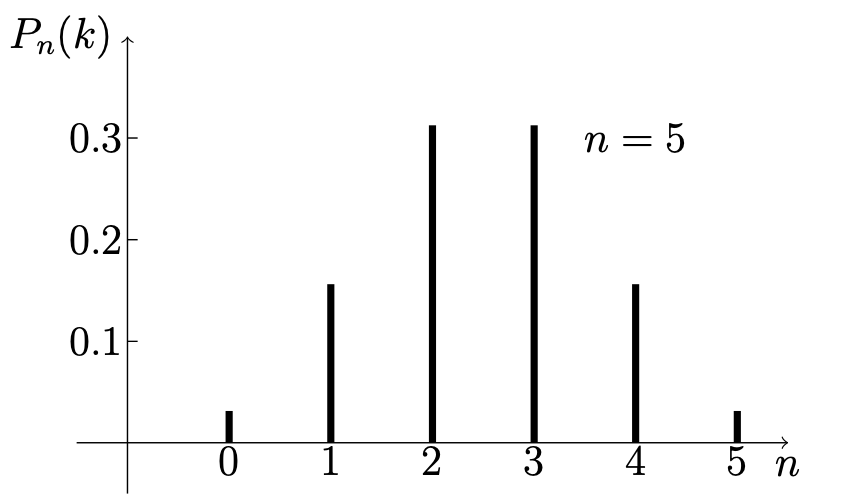
例題 1. 對於投擲對稱硬幣的情形, 我們一般假定 p = \frac {1}{2}. 若我們投擲 n 次硬幣, 記 A_{k} 為 k 次正面朝上的情形 (k = 0, 1, 2, ..., n), 則 n 次投擲中共有 k 次正面朝上的機率即為 P_{n}(k) = \mathop {\mathbf {P}}(A_{k}).

解 :

當 n = 5 時, 有 \displaystyle {\begin {cases} P_{5}(0) = \binom {0}{5} \cdot \frac {1}{2^{0}} \cdot \frac {1}{2^{5}} = \frac {1}{32}, \\ P_{5}(1) = \binom {1}{5} \cdot \frac {1}{2^{1}} \cdot \frac {1}{2^{4}} = \frac {5}{32}, \\ P_{5}(2) = \binom {2}{5} \cdot \frac {1}{2^{2}} \cdot \frac {1}{2^{3}} = \frac {10}{32}, \\ P_{5}(3) = \binom {3}{5} \cdot \frac {1}{2^{3}} \cdot \frac {1}{2^{2}} = \frac {10}{32}, \\ P_{5}(4) = \binom {4}{5} \cdot \frac {1}{2^{4}} \cdot \frac {1}{2^{1}} = \frac {5}{32}, \\ P_{5}(5) = \binom {5}{5} \cdot \frac {1}{2^{5}} \cdot \frac {1}{2^{0}} = \frac {1}{32}. \end {cases}}

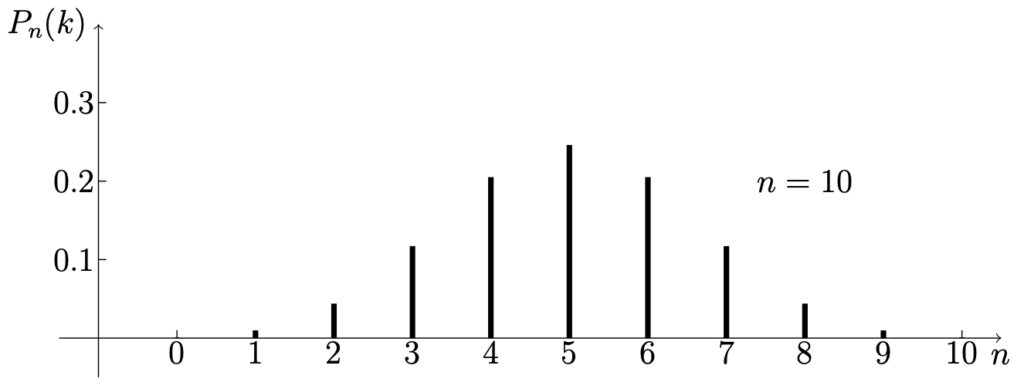
當 n = 10 時, 有 \displaystyle {\begin {cases} P_{10}(0) = \binom {0}{10} \cdot \frac {1}{2^{0}} \cdot \frac {1}{2^{10}} = \frac {1}{1024}, \\ P_{10}(1) = \binom {1}{10} \cdot \frac {1}{2^{1}} \cdot \frac {1}{2^{9}} = \frac {10}{1024}, \\ P_{10}(2) = \binom {2}{10} \cdot \frac {1}{2^{2}} \cdot \frac {1}{2^{8}} = \frac {45}{1024}, \\ P_{10}(3) = \binom {3}{10} \cdot \frac {1}{2^{3}} \cdot \frac {1}{2^{7}} = \frac {120}{1024}, \\ P_{10}(4) = \binom {4}{10} \cdot \frac {1}{2^{4}} \cdot \frac {1}{2^{6}} = \frac {210}{1024}, \\ P_{10}(5) = \binom {5}{10} \cdot \frac {1}{2^{5}} \cdot \frac {1}{2^{5}} = \frac {252}{1024}, \\ P_{10}(6) = \binom {6}{10} \cdot \frac {1}{2^{6}} \cdot \frac {1}{2^{4}} = \frac {210}{1024}, \\ P_{10}(7) = \binom {7}{10} \cdot \frac {1}{2^{7}} \cdot \frac {1}{2^{3}} = \frac {120}{1024}, \\ P_{10}(8) = \binom {8}{10} \cdot \frac {1}{2^{8}} \cdot \frac {1}{2^{2}} = \frac {45}{1024}, \\ P_{10}(9) = \binom {9}{10} \cdot \frac {1}{2^{9}} \cdot \frac {1}{2^{1}} = \frac {10}{1024}, \\ P_{10}(10) = \binom {10}{10} \cdot \frac {1}{2^{10}} \cdot \frac {1}{2^{0}} = \frac {1}{1024}. \end {cases}}

...

我們發現, 不論 n 的值如何, P_{n}(k) 的值會在 k 接近 \frac {1}{2} 時達到頂峰. 下面是二項分佈下, 幾個幾個不同的 n 最終在圖像上的表現 :

\blacksquare

例題 2. 設有一質點在直角座標系統的原點出發, 每經過單位時間就向上或者向下移動一步 :

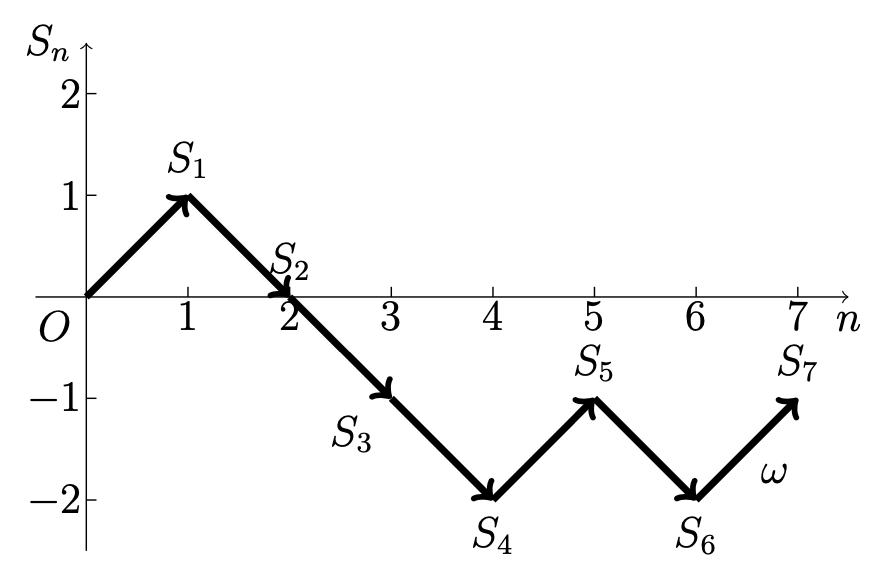
於是, 經過 n 個單位時間後, 質點移動 n 步. 顯然, 質點運動的每一條軌跡 \omega 可以用序列 (s_{1}, s_{2}, ..., s_{n}) 來表示. 對於第 i 步, 若質點向上移動, 則 s_{i} = 1; 若質點向下移動, 則 s_{i} = -1. 其中, i = 1, 2, ..., n. 現賦予每一條軌跡 \omega 以機率 \displaystyle {p(\omega) = p^{\upsilon(\omega)}q^{n - \upsilon(\omega)}}, 其中 \upsilon(\omega) 表示序列 \omega 中 s_{i} = 1 的個數, 即 \upsilon(\omega) = \frac {\sum \limits_{i = 1}^{n}s_{i} + n}{2}. 除此之外, p 和 q 都為非負實數且 p + q = 1. 由於 \sum \limits_{\omega \in \Omega}p(\omega) = 1, 可見機率組 \left \{ p(\omega) \right \} 連同軌跡 \omega = (s_{1}, s_{2}, ..., s_{n}) 的空間 \Omega 及其子集確定了質點運動的機率模型. 那麼事件 A_{k} = \left \{ \text {質點經過 } n \text { 步到達縱座標為 } k \text { 的點} \right \} 的機率如何?

解 :

一切滿足 v(\omega) - (n - v(\omega)) = k, 即 v(\omega) = \frac {n + k}{2} 的軌跡都符合問題描述. 那麼上述問題可以化約為將 \frac {n + k}{2} 個 "1" 放置到 n 個位置上, 這樣, 符合描述的軌跡共有 \begin {pmatrix} \frac {n + k}{2} \\ 2 \end {pmatrix} 條, 故有 \displaystyle {\mathop {\mathbf {P}}(A_{k}) = \binom {\frac {n + k}{2}}{n}p^{\frac {n + k}{2}}q^{n - \frac {n + k}{2}} = \binom {\frac {n + k}{2}}{n}p^{\frac {n + k}{2}}q^{\frac {n - k}{2}}}.

\blacksquare

在例題 2 中, 我們可以認為二項分佈 \displaystyle {\left \{ \mathop {\mathbf {P}}(A_{-n}), \mathop {\mathbf {P}}(A_{-(n - 1)}), ..., \mathop {\mathbf {P}}(A_{-1}), \mathop {\mathbf {P}}(A_{0}), \mathop {\mathbf {P}}(A_{1}), \mathop {\mathbf {P}}(A_{2}), ..., \mathop {\mathbf {P}}(A_{n}) \right \}} 描繪了質點移動 n 步後位置的機率分佈. 特別地, 對於 p = \frac {1}{2} 的情形, 每條軌跡的機率為 \frac {1}{2^{n}}, 於是有 \displaystyle {\mathop {\mathbf {P}}(A_{k}) = \frac {\binom {\frac {n + k}{2}}{n}}{2^{n}}}. 其中, -n \leq k \leq n. 接著, 我們來討論當 n \to \infty 時, 這些機率的漸進性質.

若令移動步伐為 2n, 由二項式係數的性質可見, 在機率 \mathop {\mathbf {P}}(A_{k})\ (|k| \leq 2n) 中的最大機率為 \displaystyle {\mathop {\mathbf {P}}(A_{0}) = \binom {n}{2n}\frac {1}{2^{2n}} = \frac {(2n)!}{(n!)^{2}} \cdot \frac {1}{2^{2n}}}. 根據 Stirling 公式, 我們知道 n! \doteq \sqrt {2\pi n}\left ( \frac {n}{e} \right )^{n}. 因此, 對於充分大的 n, 有 \displaystyle {\mathop {\mathbf {P}}(A_{0}) \doteq \frac {1}{\sqrt {\pi n}}}.

2. 多項分佈

現在, 我們推廣二項分佈的機率模型. 假設基本事件空間有如下構造 : \displaystyle {\Omega = \left \{ \omega : \omega = (a_{1}, a_{2}, ..., a_{n}), a_{i} = b_{1}, b_{2}, ..., b_{r}\ (i = 1, 2, ..., n) \right \}}. 其中, b_{1}, b_{2}, ..., b_{r} 都是給定的數. 設 \upsilon_{i}(\omega) 是序列 \omega = (a_{1}, a_{2}, ..., a_{n}) 中等於 b_{i}\ (i = 1, 2, ..., r) 元素的數量, 而基本事件 \omega 有機率 \displaystyle {p(\omega) = p_{1}^{\upsilon_{1}(\omega)}p_{2}^{v_{2}(\omega)}...p_{r}^{\upsilon_{r}(\omega)}} 其中, p_{i} \geq 0\ (i = 1, 2, ..., r), p_{1} + p_{2} + ... + p_{r} = 1. 為了說明推廣後的情形仍然合理, 我們首先注意到 \displaystyle {\sum \limits_{\omega \in \Omega}p(\omega) = \sum \limits_{ \left \{ \begin {gathered} \scriptsize {n_{1} \geq 0, n_{2} \geq 0, ..., n_{r} \geq 0} \\ \scriptsize {n_{1} + n _{2} + ... + n_{r} = n} \end {gathered} \right \}} \binom {n_{1}, n_{2}, ..., n_{r}}{n}p_{1}^{n_{1}}p_{2}^{n_{2}}...p_{r}^{n_{r}}}. 上式中, \binom {n_{1}, n_{2}, ..., n_{r}}{n} 表示有序序列 (a_{1}, a_{2}, ..., a_{n}) 的數量. 其中, 元素 b_{1} 重複 n_{1} 次, 元素 b_{2} 重複 n_{2} 次, ..., 元素 b_{r} 重複 n_{r} 次. 由於共有 \binom {n_{1}}{n} 種方法將元素 b_{1} 放置在 n 個位置上, 共有 \binom {n_{2}}{n} 種方法將元素 b_{2} 放置在 n 個位置上, ..., 共有 \binom {n_{r}}{n} 種方法將元素 b_{r} 放置在 n 個位置上, 所以 \displaystyle {\begin {aligned} \binom {n_{1}, n_{2}, ..., n_{r}}{n} &= \binom {n_{1}}{n}\binom {n_{2}}{n - n_{1}}...\binom {n_{r}}{n - (n_{1} + n_{2} + ... n_{r - 1})} \\ &= \frac {n!}{n_{1}!(n - n_{1})!} \times \frac {n!}{n_{2}!(n - n_{1} - n_{2})!} \times ... \times 1 \\ &= \frac {n!}{n_{1}!n_{2}!...n_{r}!}. \end {aligned}} 故 \displaystyle {\begin {aligned} \sum \limits_{\omega \in \Omega}p(\omega) &= \sum \limits_{ \left \{ \begin {gathered} \scriptsize {n_{1} \geq 0, n_{2} \geq 0, ..., n_{r} \geq 0} \\ \scriptsize {n_{1} + n _{2} + ... + n_{r} = n} \end {gathered} \right \}} \binom {n_{1}, n_{2}, ..., n_{r}}{n}p_{1}^{n_{1}}p_{2}^{n_{2}}...p_{r}^{n_{r}} \\ &= (p_{1} + p_{2} + ... + p_{r})^{n} = 1. \end {aligned}} 因此, 針對二項分佈推廣後的分佈仍然是機率分佈.

設 \displaystyle {A_{n_{1}, n_{2}, ..., n_{r}} = \left \{ \omega : \upsilon_{1}(\omega) = n_{1}, \upsilon_{2}(\omega) = n_{2}, ..., \upsilon_{r}(\omega) = n_{r} \right \}}, 則 \displaystyle {\mathop {\mathbf {P}}(A_{n_{1}, n_{2}, ..., n_{r}}) = \binom {n_{1}, n_{2}, ..., n_{r}}{n}p_{1}^{n_{1}}p_{2}^{n_{2}}...p_{r}^{n_{r}}}. 機率組 \{ \mathop {\mathbf {P}}(A_{n_{1}, n_{2}, ..., n_{r}}) \} 稱為多項分佈 (multinomial distribution). 而二項分佈是 r = 2 時多項分佈的特例.

3. 多元超幾何分佈

例題 3. 假設一箱子中有編號為 1, 2, ..., n 的 n 個不同的球. 其中, n_{1} 個球具有顏色 c_{1}, n_{2} 個球具有顏色 c_{2}, ..., n_{r} 個球具有顏色 c_{r}, n_{1} + n_{2} + ... + n_{r} = n. 現在從箱中進行 m 次不放回抽樣 (m < n). 基本事件空間為 \displaystyle {\begin {aligned} \Omega = \{ &\omega : \omega = (a_{1}, a_{2}, ..., a_{m}), a_{k} \neq a_{l}, k, l = 1, 2, ..., m, k \neq l, \\ &\ \ \ \ a_{i} = 1, 2, ..., n \ (i = 1, 2, ..., m) \}. \end {aligned}} 顯然, \mathop {\mathrm {card}}{\Omega} = (n)_{m}. 假設基本事件都是等可能的, 而事件 B_{m_{1}, m_{2}, ..., m_{r}} = \{ m_{1} \text { 個球具有顏色 } c_{1}, m_{2} \text { 個球具有顏色 } c_{2}, ..., m_{r} \text { 個球具有顏色 } c_{r}, m_{1} + m_{2} + ... + m_{r} = m \} 的機率如何?

解 :

從 n_{i} 個具有顏色 c_{i} 的球中抽出 m_{i} 個, 共有 \binom {m_{i}}{n_{i}} 種可能的結局. 其中, i = 1, 2, ..., r. 故有 \displaystyle {\mathop {\mathrm {card}}{\left \{ B_{m_{1}, m_{2}, ..., m_{r}} \right \}} = \binom {m_{1}}{n_{1}}\binom {m_{2}}{n_{2}}...\binom {m_{r}}{n_{r}} }. 因此, \displaystyle {\mathop {\mathbf {P}}(B_{m_{1}, m_{2}, ..., m_{r}}) = \frac {\mathop {\mathrm {card}}{\left \{ B_{m_{1}, m_{2}, ..., m_{r}} \right \}}}{\mathop {\mathrm {card}}{\Omega}} = \frac {\binom {m_{1}}{n_{1}}\binom {m_{2}}{n_{2}}...\binom {m_{r}}{n_{r}}}{\binom {m}{n}}}

\blacksquare

機率組 \{ B_{m_{1}, m_{2}, ..., m_{r}} \} 稱為多元超幾何分布 (multivariate hypergeometric distribution). 當 r = 2 時, 多元超幾何分布退化為超幾何分布 (hypergeometric distribution), 其母函數為超幾何函數.

多元超幾何分布的構造相當複雜, 當 r = 2 時, \displaystyle {\mathop {\mathbf {P}}(B_{m_{1}}, B_{m_{2}}) = \frac {\binom {m_{1}}{n_{1}}\binom {m_{2}}{n_{2}}}{\binom {m_{1} + m _{2}}{n_{1} + n_{2}}}, n_{1} + n_{2} = n, m_{1} + m_{2} = m}. 其中包含了九階乘數. 當 n \to \infty, n_{1} \to \infty 且 \frac {n_{1}}{n} \to p 時, 有 \frac {n_{2}}{n} \to 1 - p. 根據斯特靈公式, 可以得到 \displaystyle {\mathop {\mathbf {P}}(B_{m_{1}}, B_{m_{2}}) \doteq \binom {m_{2}}{m_{1} + m_{2}} p^{m_{1}}(1 - p)^{m_{2}}}, 即當 n \to \infty, n_{1} \to \infty 且 \frac {n_{1}}{n} \to p 時, 超幾何分布逼近二項分布. 從直觀上來說, 這也是明顯的. 因為當 n 和 n_{1} 充分大但是有限時, 不放回抽樣得到的結果幾乎和放回抽樣時一樣的.

4. 練習題

自主習題 1. 證明 : 對於多項分布的機率, 若且唯若點 (k_{1}, k_{2}, ..., k_{r}) 在滿足 \displaystyle {np_{i} - 1 <k_{i} \leq (n + r - 1)p_{i}} 時達到最大值. 其中, i = 1, 2, ..., r.

自主習題 2. 假設 N 是某個總體的容量, 要求在對總體的全部元素沒有簡單重複計數的情況下, 以最少的成本去估計 N 的大小. 例如, 在估計某個地區或者國家的人口等類似問題. Pierre-Simon Laplace 在 1786 年法國人口為 N 時, 提出過以下方法 : 從總體中選擇 m 個元素, 並且做上標記. 然後將這 m 個元素放回原總體, 並且與無標記的元素均衡混合. 然後從混合後的總體中再抽取 n 個元素, 其中有 x 個元素帶有標記.

1. 證明 : 由超幾何分布的公式 \mathop {\mathbf {P}}(B_{m_{1}}, B_{m_{2}}) = \frac {\binom {m_{1}}{n_{1}}\binom {m_{2}}{n_{2}}}{\binom {m_{1} + m _{2}}{n_{1} + n_{2}}}, n_{1} + n_{2} = n, m_{1} + m_{2} = m, 相應的機率 \mathop {\mathbf {P}}_{N, m, n} \{ X = m \} 可以表示為 \displaystyle {\mathop {\mathbf {P}}_{N, m, n} \left \{ X = M \right \} = \frac {\binom {n}{m}\binom {n - M}{N - M}}{\binom {n}{N}}}.
2. 假設 m, n 和 m 固定, 對 N 求上面機率的最大值, 即求總體的極大概似 (maximum likelihood) 容量 N, 使得對於給定的 m 和 n, 有標記的元素個數 X = M.
3. 證明 : 對總體容量的極大概似估計值, 不妨記為 \hat {N}, 有 \displaystyle {\hat {N} = \left \lfloor \frac {nm}{M} \right \rfloor}.

這樣得到的估計量 \hat {N} 稱作 N 的極大概似估計 (maximum likelihood estimation).